UIUCTF2024

Crypto

X Marked the Spot

题目

from itertools import cycle

flag = b"uiuctf{????????????????????????????????????????}"
# len(flag) = 48
key  = b"????????"
# len(key) = 8
ct = bytes(x ^ y for x, y in zip(flag, cycle(key)))

with open("ct", "wb") as ct_file:
    ct_file.write(ct)

简单的异或算法
根据uiuctf{}拿到key，因为我们一开始就可以获取到key的前七位，而正好flag的长度为48，所以最后的}，可以帮我们确认key的最后一位

from pwn import *
with open("ct", 'rb')as cipher:
    m = cipher.read()
    k = b'uiuctf{'
    for i in range(7):
        print(chr(m[i] ^ k[i]), end='')
    print(chr(m[-1] ^ ord('}')))
    key = b'hdiqbfjq'
    print(xor(m, key))

Without a Trace

题目

import numpy as np
from Crypto.Util.number import bytes_to_long
from itertools import permutations


def inputs():
    print("[WAT] Define diag(u1, u2, u3. u4, u5)")
    M = [
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
    ]
    for i in range(5):
        try:
            M[i][i] = int(input(f"[WAT] u{i + 1} = "))
        except:
            return None
    return M


def handler(signum, frame):
    raise Exception("[WAT] You're trying too hard, try something simpler")


def check(M):
    def sign(sigma):
        l = 0
        for i in range(5):
            for j in range(i + 1, 5):
                if sigma[i] > sigma[j]:
                    l += 1
        return (-1)**l

    res = 0
    for sigma in permutations([0, 1, 2, 3, 4]):
        curr = 1
        for i in range(5):
            curr *= M[sigma[i]][i]
        res += sign(sigma) * curr
    return res


def fun(M):
    FLAG = 'uiuctf{}'
    f = [bytes_to_long(bytes(FLAG[5*i:5*(i+1)], 'utf-8')) for i in range(5)]
    F = [
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
    ]
    for i in range(5):
        F[i][i] = f[i]

    try:
        R = np.matmul(F, M)
        return np.trace(R)

    except:
        print("[WAT] You're trying too hard, try something simpler")
        return None


def main():
    print("[WAT] Welcome")
    M = inputs()
    if M is None:
        print("[WAT] You tried something weird...")
        return
    elif check(M) == 0:
        print("[WAT] It's not going to be that easy...")
        return

    res = fun(M)
    if res == None:
        print("[WAT] You tried something weird...")
        return
    print(f"[WAT] Have fun: {res}")


if __name__ == "__main__":
    main()

分析一下代码，我们输入5*5矩阵的对角元素，同时这个矩阵会被check，flag分为5部分，也排布在5*5矩阵的对角上，然后两个矩阵相乘，最后返回轨迹，即对角线上的元素之和

由于检测的存在，不能直接获取到一部分的flag，但可以通过运算或得
发送6次对角元素，直接手动交互

[
    [1,1,1,1,1],
    [2,1,1,1,1],
    [1,2,1,1,1],
    [1,1,2,1,1],
    [1,1,1,2,1],
    [1,1,1,1,2]
]

简单题

from Crypto.Util.number import *

fun = [2504408575853, 2440285994541,
       2426159182680, 2163980646766, 2465934208374]
a = 2000128101369
for f in fun:
    print(long_to_bytes(f-a))
# uiuctf{tr4c1ng_&&_mult5!}

Naptime

题目

from random import randint
from Crypto.Util.number import getPrime, bytes_to_long, long_to_bytes
import numpy as np

def get_b(n):
    b = []
    b.append(randint(2**(n-1), 2**n))
    for i in range(n - 1):
        lb = sum(b)
        found = False
        while not found:
            num = randint(max(2**(n + i), lb + 1), 2**(n + i + 1))
            if num > lb:
                found = True
                b.append(num)

    return b

def get_MW(b):
    lb = sum(b)
    M = randint(lb + 1, 2*lb)
    W = getPrime(int(1.5*len(b)))

    return M, W

def get_a(b, M, W):
    a_ = []
    for num in b:
        a_.append(num * W % M)
    pi = np.random.permutation(list(i for i in range(len(b)))).tolist()
    a = [a_[pi[i]] for i in range(len(b))]
    return a, pi


def enc(flag, a, n):
    bitstrings = []
    for c in flag:
        # c -> int -> 8-bit binary string
        bitstrings.append(bin(ord(c))[2:].zfill(8))
    ct = []
    for bits in bitstrings:
        curr = 0
        for i, b in enumerate(bits):
            if b == "1":
                curr += a[i]
        ct.append(curr)

    return ct

def dec(ct, a, b, pi, M, W, n):
    # construct inverse permuation to pi
    pii = np.argsort(pi).tolist()
    m = ""
    U = pow(W, -1, M)
    ct = [c * U % M for c in ct]
    for c in ct:
        # find b_pi(j)
        diff = 0
        bits = ["0" for _ in range(n)]
        for i in reversed(range(n)):
            if c - diff > sum(b[:i]):
                diff += b[i]
                bits[pii[i]] = "1"
        # convert bits to character
        m += chr(int("".join(bits), base=2))

    return m


def main():
    flag = 'uiuctf{I_DID_NOT_LEAVE_THE_FLAG_THIS_TIME}'

    # generate cryptosystem
    n = 8
    b = get_b(n)
    M, W = get_MW(b)
    a, pi = get_a(b, M, W)

    # encrypt
    ct = enc(flag, a, n)

    # public information
    print(f"{a =  }")
    print(f"{ct = }")

    # decrypt
    res = dec(ct, a, b, pi, M, W, n)

if __name__ == "__main__":
    main()

一开始我还想，逆推加密函数，根据ct在a中的加算组合，来确定flag的二进制序列，发现GPT写的回溯算法应该是行不通的，然后看了一下群里师傅的思路，又再仔细读了一下代码，下面是我的思路

可以看到给出了加解密函数，还有一些辅助函数，如果我们可以得到参数b,pi,M,W，那么就可以利用解密函数来解密密文了
pi = np.random.permutation(list(i for i in range(len(b)))).tolist()，是一个排列组合，可以用b来爆破一手，那么缺的就是三个参数了
通过读懂程序，我们可以判断到M和W的位数，然后根据题目提供的a，爆破出M和W的可能取值，b的话得重新生成，再进行递增排序(根据生成b的函数可知)

恰好拿到的第一组M和W，以及根据pi爆破flag，得到了正确的flag

from random import randint
from pwn import *
from Crypto.Util.number import *
import numpy as np
a_list = [66128, 61158, 36912, 65196, 15611, 45292, 84119, 65338]
ct = [273896, 179019, 273896, 247527, 208558, 227481, 328334, 179019, 336714, 292819, 102108, 208558, 336714, 312723, 158973, 208700, 208700, 163266, 244215,
      336714, 312723, 102108, 336714, 142107, 336714, 167446, 251565, 227481, 296857, 336714, 208558, 113681, 251565, 336714, 227481, 158973, 147400, 292819, 289507]
n = 8
"""
for M in range(2**15, 2**16):
    for W in range(2**11, 2**12):
        if not isPrime(W):
            continue
        f = [0, 0, 0, 0, 0, 0, 0, 0]
        for a in a_list:
            if GCD(W, M) == 1:
                b = inverse(W, M)*a % M
                if b.bit_length() == 8:
                    f[0] = 1
                if b.bit_length() == 9:
                    f[1] = 1
                if b.bit_length() == 10:
                    f[2] = 1
                if b.bit_length() == 11:
                    f[3] = 1
                if b.bit_length() == 12:
                    f[4] = 1
                if b.bit_length() == 13:
                    f[5] = 1
                if b.bit_length() == 14:
                    f[6] = 1
                if b.bit_length() == 15:
                    f[7] = 1
        if sum(f) == 8:
            print(W)
            print(M)
"""
def dec(ct, a, b, pi, M, W, n):
    # construct inverse permuation to pi
    pii = np.argsort(pi).tolist()
    m = ""
    U = pow(W, -1, M)
    ct = [c * U % M for c in ct]
    for c in ct:
        # find b_pi(j)
        diff = 0
        bits = ["0" for _ in range(n)]
        for i in reversed(range(n)):
            if c - diff > sum(b[:i]):
                diff += b[i]
                bits[pii[i]] = "1"
        # convert bits to character
        m += chr(int("".join(bits), base=2))
    return m
W = 2557
M = 38755
b = []
for a in a_list:
    b.append(inverse(W, M)*a % M)
b = sorted(b)
while 1:
    pi = np.random.permutation(list(i for i in range(len(b)))).tolist()
    flag = dec(ct, a_list, b, pi, M, W, n)
    if 'uiuctf{' in flag:
        print(flag)
        break

后来看到了狼组的wp，发现还真可以用背包问题求解，但是我不会写，下面是他们的wp

from Crypto.Util.number import *
def solve(ww):
    a =  [66128, 61158, 36912, 65196, 15611, 45292, 84119, 65338]
    ct = [273896, 179019, 273896, 247527, 208558, 227481, 328334, 179019, 336714, 292819, 102108, 208558, 336714, 312723, 158973, 208700, 208700, 163266, 244215, 336714, 312723, 102108, 336714, 142107, 336714, 167446, 251565, 227481, 296857, 336714, 208558, 113681, 251565, 336714, 227481, 158973, 147400, 292819, 289507]
    C = ct[ww]
    M = a
    pk = M
    ct = C
    n = len(pk)

    # Sanity check for application of low density attack
    d = n / log(max(pk), 2)
    assert CDF(d) < 0.9408
    M = Matrix.identity(n) * 2

    last_row = [1 for x in pk]
    M_last_row = Matrix(ZZ, 1, len(last_row), last_row)

    last_col = pk
    last_col.append(ct)
    M_last_col = Matrix(ZZ, len(last_col), 1, last_col)

    M = M.stack(M_last_row)
    M = M.augment(M_last_col)

    X = M.BKZ()

    sol = []
    for i in range(n + 1):
        testrow = X.row(i).list()[:-1]
        if set(testrow).issubset([-1, 1]):
            for v in testrow:
                if v == 1:
                    sol.append(0)
                elif v == -1:
                    sol.append(1)
            break

    s = sol
    return s
ct = [273896, 179019, 273896, 247527, 208558, 227481, 328334, 179019, 336714, 292819, 102108, 208558, 336714, 312723, 158973, 208700, 208700, 163266, 244215, 336714, 312723, 102108, 336714, 142107, 336714, 167446, 251565, 227481, 296857, 336714, 208558, 113681, 251565, 336714, 227481, 158973, 147400, 292819, 289507]
flag=''
for ee in range(len(ct)):
    rr=solve(ee)
    pp=''
    for tt in rr:
        pp+=str(tt)
    flag+=chr(int(pp,2))
print(flag)

Determined

看题目貌似是算行列式(det)?

from Crypto.Util.number import bytes_to_long, long_to_bytes
from itertools import permutations
from SECRET import FLAG, p, q, r



def inputs():
    print("[DET] First things first, gimme some numbers:")
    M = [
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
    ]
    try:
        M[0][0] = p
        M[0][2] = int(input("[DET] M[0][2] = "))
        M[0][4] = int(input("[DET] M[0][4] = "))

        M[1][1] = int(input("[DET] M[1][1] = "))
        M[1][3] = int(input("[DET] M[1][3] = "))

        M[2][0] = int(input("[DET] M[2][0] = "))
        M[2][2] = int(input("[DET] M[2][2] = "))
        M[2][4] = int(input("[DET] M[2][4] = "))

        M[3][1] = q
        M[3][3] = r

        M[4][0] = int(input("[DET] M[4][0] = "))
        M[4][2] = int(input("[DET] M[4][2] = "))
    except:
        return None
    return M

def handler(signum, frame):
    raise Exception("[DET] You're trying too hard, try something simpler")

def fun(M):
    def sign(sigma):
        l = 0
        for i in range(5):
            for j in range(i + 1, 5):
                if sigma[i] > sigma[j]:
                    l += 1
        return (-1)**l

    res = 0
    for sigma in permutations([0,1,2,3,4]):
        curr = 1
        for i in range(5):
            curr *= M[sigma[i]][i]
        res += sign(sigma) * curr
    return res

def main():
    print("[DET] Welcome")
    M = inputs()
    if M is None:
        print("[DET] You tried something weird...")
        return

    res = fun(M)
    print(f"[DET] Have fun: {res}")

if __name__ == "__main__":
    main()

def fun(M):
    def sign(sigma):
        l = 0
        for i in range(5):
            for j in range(i + 1, 5):
                if sigma[i] > sigma[j]:
                    l += 1
        return (-1)**l

    res = 0
    for sigma in permutations([0,1,2,3,4]):
        curr = 1
        for i in range(5):
            curr *= M[sigma[i]][i]
        res += sign(sigma) * curr
    return res

此处的fun()应该是用来计算五阶行列式的

因为我们可以控制元素为0，所以我们可以控制想要的行列式值
我们可以计算这样的一个矩阵的行列式

[
    p 0 0 0 0
    0 1 0 0 0
    0 0 1 0 1
    0 q 0 r 0
    0 0 1 0 0
]

按一二行展开，就成了计算

[
    p 0
    0 1
]
*
[
    1 0 1
    0 r 0
    1 0 0
]

则Det(M)=-p*r
gcd一下n，便可得到p

from Crypto.Util.number import *
n = 158794636700752922781275926476194117856757725604680390949164778150869764326023702391967976086363365534718230514141547968577753309521188288428236024251993839560087229636799779157903650823700424848036276986652311165197569877428810358366358203174595667453056843209344115949077094799081260298678936223331932826351
e = 65535
c = 72186625991702159773441286864850566837138114624570350089877959520356759693054091827950124758916323653021925443200239303328819702117245200182521971965172749321771266746783797202515535351816124885833031875091162736190721470393029924557370228547165074694258453101355875242872797209141366404264775972151904835111
pr = 89650932835934569650904059412290773134844226367466628096799329748763412779644167490959554682308225788447301887591344484909099249454270292467079075688237075940004535625835151778597652605934044472146068875065970359555553547536636518184486497958414801304532202276337011187961205104209096129018950458239166991017
p = GCD(n, pr)
q = n//p
phi = (q-1)*(p-1)
d = inverse(e, phi)
print(long_to_bytes(pow(c, d, n)))

Crypto(未解)

以下由于时间关系，或者说难度，就暂时没有做了

Snore Signatures

题目

#!/usr/bin/env python3

from Crypto.Util.number import isPrime, getPrime, long_to_bytes, bytes_to_long
from Crypto.Random.random import getrandbits, randint
from Crypto.Hash import SHA512

LOOP_LIMIT = 2000


def hash(val, bits=1024):
    output = 0
    for i in range((bits//512) + 1):
        h = SHA512.new()
        h.update(long_to_bytes(val) + long_to_bytes(i))
        output = int(h.hexdigest(), 16) << (512 * i) ^ output
    return output


def gen_snore_group(N=512):
    q = getPrime(N)
    for _ in range(LOOP_LIMIT):
        X = getrandbits(2*N)
        p = X - X % (2 * q) + 1
        if isPrime(p):
            break
    else:
        raise Exception("Failed to generate group")

    r = (p - 1) // q

    for _ in range(LOOP_LIMIT):
        h = randint(2, p - 1)
        if pow(h, r, p) != 1:
            break
    else:
        raise Exception("Failed to generate group")

    g = pow(h, r, p)

    return (p, q, g)


def snore_gen(p, q, g, N=512):
    x = randint(1, q - 1)
    y = pow(g, -x, p)
    return (x, y)


def snore_sign(p, q, g, x, m):
    k = randint(1, q - 1)
    r = pow(g, k, p)
    e = hash((r + m) % p) % q
    s = (k + x * e) % q
    return (s, e)


def snore_verify(p, q, g, y, m, s, e):
    if not (0 < s < q):
        return False

    rv = (pow(g, s, p) * pow(y, e, p)) % p
    ev = hash((rv + m) % p) % q

    return ev == e


def main():
    p, q, g = gen_snore_group()
    print(f"p = {p}")
    print(f"q = {q}")
    print(f"g = {g}")

    queries = []
    for _ in range(10):
        x, y = snore_gen(p, q, g)
        print(f"y = {y}")

        print('you get one query to the oracle')

        m = int(input("m = "))
        queries.append(m)
        s, e = snore_sign(p, q, g, x, m)
        print(f"s = {s}")
        print(f"e = {e}")

        print('can you forge a signature?')
        m = int(input("m = "))
        s = int(input("s = "))
        # you can't change e >:)
        if m in queries:
            print('nope')
            return
        if not snore_verify(p, q, g, y, m, s, e):
            print('invalid signature!')
            return
        queries.append(m)
        print('correct signature!')

    print('you win!')
    print(open('flag.txt').read())

if __name__ == "__main__":
    main()

These signatures are a bore!

ncat --ssl snore-signatures.chal.uiuc.tf 1337

Groups

题目

from random import randint
from math import gcd, log
import time
from Crypto.Util.number import *


def check(n, iterations=50):
    if isPrime(n):
        return False

    i = 0
    while i < iterations:
        a = randint(2, n - 1)
        if gcd(a, n) == 1:
            i += 1
            if pow(a, n - 1, n) != 1:
                return False
    return True


def generate_challenge(c):
    a = randint(2, c - 1)
    while gcd(a, c) != 1:
        a = randint(2, c - 1)
    k = randint(2, c - 1)
    return (a, pow(a, k, c))


def get_flag():
    with open('flag.txt', 'r') as f:
        return f.read()

if __name__ == '__main__':
    c = int(input('c = '))

    if log(c, 2) < 512:
        print(f'c must be least 512 bits large.')
    elif not check(c):
        print(f'No cheating!')
    else:
        a, b = generate_challenge(c)
        print(f'a = {a}')
        print(f'a^k = {b} (mod c)')
        
        k = int(input('k = '))

        if pow(a, k, c) == b:
            print(get_flag())
        else:
            print('Wrong k')

My friend told me that cryptography is unbreakable if moduli are Carmichael numbers instead of primes. I decided to use this CTF to test out this theory.

ncat --ssl groups.chal.uiuc.tf 1337

Key in a Haystack

题目

from Crypto.Util.number import getPrime
from Crypto.Util.Padding import pad
from Crypto.Cipher import AES

from hashlib import md5
from math import prod
import sys

from secret import flag

key = getPrime(40)
haystack = [ getPrime(1024) for _ in range(300) ]
key_in_haystack = key * prod(haystack)

enc_flag = AES.new(
    key = md5(b"%d" % key).digest(),
    mode = AES.MODE_ECB
).encrypt(pad(flag, 16))

sys.set_int_max_str_digits(0)

print(f"enc_flag: {enc_flag.hex()}")
print(f"haystack: {key_in_haystack}")

exit(0)

I encrpyted the flag, but I lost my key in an annoyingly large haystack. Can you help me find it and decrypt the flag?

ncat --ssl key-in-a-haystack.chal.uiuc.tf 1337

Web

Fare Evasion()

靶机地址
https://fare-evasion.chal.uiuc.tf/

逃票

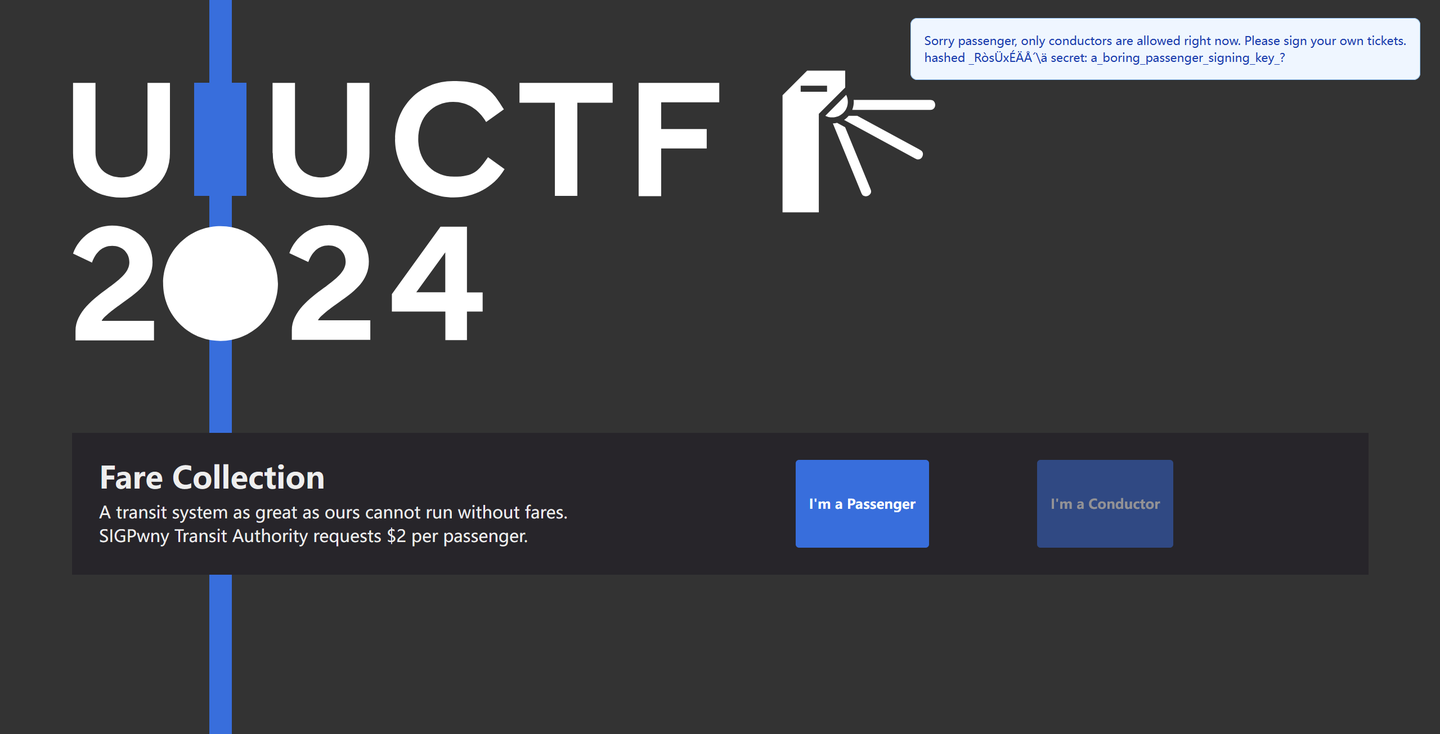
感觉是JWT伪造，试了一下，好像也不是啊

看一眼前端这个buttonI'm a Conductor，改了一下，没有用

async function pay() {
      // i could not get sqlite to work on the frontend :(
      /*
        db.each(`SELECT * FROM keys WHERE kid = '${md5(headerKid)}'`, (err, row) => {
        ???????
       */
      const r = await fetch("/pay", { method: "POST" });
      const j = await r.json();
      document.getElementById("alert").classList.add("opacity-100");
      // todo: convert md5 to hex string instead of latin1??
      document.getElementById("alert").innerText = j["message"];
      setTimeout(() => { document.getElementById("alert").classList.remove("opacity-100") }, 5000);
    }

然后，是这个pay()函数
这里的sql注入和md5应该是有用处的，从返回的包的结果来看，思路应该还是要回到JWT伪造上，然后卡住……

Web又没得玩。。。。。
然后这misc好像确实是有难度的，不用打了，下班

又是只能做做密码的一天…………